
| A. | 1 | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{13}$ |
分析 可知,$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,根据条件对上式两边平方进行数量积的运算即可得出${\overrightarrow{BC}}^{2}$,从而得出$|\overrightarrow{BC}|$的值.
解答 解:${\overrightarrow{BC}}^{2}=(\overrightarrow{AC}-\overrightarrow{AB})^{2}$
=${\overrightarrow{AC}}^{2}-2\overrightarrow{AC}•\overrightarrow{AB}+{\overrightarrow{AB}}^{2}$
=$9-2×3×1×\frac{1}{2}+1$
=7;
∴$|\overrightarrow{BC}|=\sqrt{7}$.
故选:B.
点评 考查向量减法的几何意义,以及向量数量积的运算及计算公式,要求$|\overrightarrow{BC}|$,而求$|\overrightarrow{BC}{|}^{2}$的方法.


科目:高中数学 来源: 题型:解答题
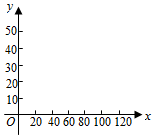 在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:
在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:| x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若求得相关系数r=-0.89,则y与x具备很强的线性相关关系,且为负相关 | |
| B. | 同学甲根据这组数据得到的回归模型1的残差平方和E1=1.8,同学乙根据这组数据得到的回归模型2的残差平方和E2=2.4,则模型1的拟合效果更好 | |
| C. | 用相关指数R2来刻画回归效果,模型1的相关指数R12=0.48,模型2的相关指数R22=0.91,则模型1的拟合效果更好 | |
| D. | 该回归分析只对被调查样本的总体适用 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{3}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | (-$\frac{π}{2}$,$\frac{π}{6}$) | D. | (-$\frac{π}{2}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<b2 | C. | ac2<bc2 | D. | a2>ab>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com