
| A. | 是偶函数,而非奇函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是奇函数,而非偶函数 | D. | 是非奇非偶函数 |
分析 先求出函数的定义域关于原点对称,再根据在函数的定义域内,f(-x)=-f(x)恒成立,可得函数为奇函数.
解答 解:∵$f(x)=\frac{{\sqrt{1-{x^2}}}}{|x+3|-3}$,∴$\left\{\begin{array}{l}{1{-x}^{2}≥0}\\{|x+3|≠3}\end{array}\right.$,求得-1<x<0,或0<x<1,
故函数的定义域为{x|-1<x<0,或0<x<1 },关于原点对称,
再根据f(-x)=$\frac{\sqrt{{1-x}^{2}}}{|-x+3|-3}$=$\frac{\sqrt{{1-x}^{2}}}{|x-3|-3}$≠-f(x),
当0<x<1时,f(x)=$\frac{\sqrt{{1-x}^{2}}}{x}$,f(-x)=$\frac{\sqrt{{1-x}^{2}}}{-x}$=-f(x);
当-1<x<0时,f(x)=$\frac{\sqrt{{1-x}^{2}}}{x}$,f(-x)=$\frac{\sqrt{{1-x}^{2}}}{-x}$=-f(x);
故在函数的定义域内,f(-x)=-f(x)恒成立,故函数为奇函数,
故选:C.
点评 本题主要考查函数的奇偶性的判断方法,属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气污染指数 (单位:μg/m3) | (0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
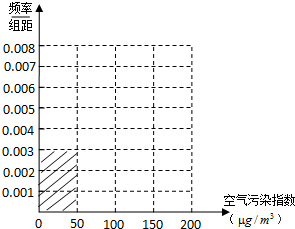
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
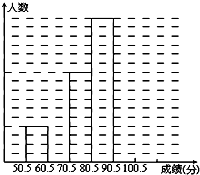 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | a | 0.16 |
| 70.5~80.5 | 10 | b |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | c | d |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|1<x≤4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com