
分析 (1)由椭圆过点M($\sqrt{2}$,1),且焦点为F1(-$\sqrt{2}$,0),列出方程组求出a,b,由此能求出椭圆C的方程.
(2)设点Q(x,y),A(x1,y1),B(x2,y2),设$\overrightarrow{PA}$=-$λ\overrightarrow{AQ}$,$\overrightarrow{PB}=λ\overrightarrow{BQ}$,(λ≠0,±1),利用点差法能证明点Q总在直线上.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M($\sqrt{2}$,1),且焦点为F1(-$\sqrt{2}$,0),
∴由题意$\left\{\begin{array}{l}{{c}^{2}=2}\\{\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{c}^{2}={a}^{2}-{b}^{2}}\end{array}\right.$,解得a2=4,b2=2,
∴所求的椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
(2)设点Q(x,y),A(x1,y1),B(x2,y2),
由题设,|$\overrightarrow{PA}$|、|$\overrightarrow{PB}$|、|$\overrightarrow{AQ}$|、|$\overrightarrow{QB}$|均不为0,且满足$\frac{|\overrightarrow{AP}|}{|\overrightarrow{PB}|}$=$\frac{|\overrightarrow{AQ}|}{|\overrightarrow{QB}|}$,
又P、A、Q、B四点共线,设$\overrightarrow{PA}$=-$λ\overrightarrow{AQ}$,$\overrightarrow{PB}=λ\overrightarrow{BQ}$,(λ≠0,±1),
∴${x}_{1}=\frac{4-λx}{1-λ}$,${y}_{1}=\frac{-λy}{1-λ}$,①
${x}_{2}=\frac{4+λx}{1+λ}$,${y}_{2}=\frac{λy}{1+λ}$,②
∵A(x1,y1),B(x2,y2)在椭圆上,
将①②分别代入C的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,整理得:
(x2+2y2-4)λ2-8(x-1)λ+12=0,③
(x2+2y2-4)λ2+8(x-1)λ+12=0,④
由④-③,得-8(x-1)λ=0,
∵λ≠0,∴x-1=0,
即点Q(x,y)总在直线x-1=0上.
点评 本题考查椭圆方程的求法,考查点在定直线上的证明,是中档题,解题时要认真审题,注意点差法和椭圆性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[\frac{1}{2},1)$ | C. | $[\frac{{\sqrt{3}}}{2},1)$ | D. | $[\frac{{\sqrt{2}}}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
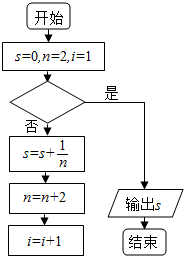
| A. | i>2016 | B. | i<2016 | C. | i>1008 | D. | i<1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com