
分析 设A(x1,y1),B(x2,y2),代入抛物线的方程,作差,运用直线的斜率公式和中点坐标公式,可得斜率,再由点斜式方程可得直线AB的方程.
解答 解:设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}x_1^2=4{y_1}\\ x_2^2=4{y_2}\end{array}\right.$⇒(x1-x2)(x1+x2)=4(y1-y2),
∵$\frac{{{x_1}+{x_2}}}{2}=1⇒{x_1}+{x_2}=2$,
∴${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{2}{4}=\frac{1}{2}$,
∴直线l的方程为y-2=$\frac{1}{2}$(x-1),即为l:x-2y+3=0.
点评 本题考查抛物线的方程及运用,考查点差法的运用,以及直线的斜率公式和中点坐标公式,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$) | B. | (-$\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$) | C. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | D. | (-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{9}^{3}$ | B. | A${\;}_{9}^{3}$ | C. | A${\;}_{9}^{6}$ | D. | A${\;}_{9}^{3}$•A${\;}_{3}^{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 种下一粒杨树种子,求其能长成大树的概率 | |
| B. | 掷一颗质地不均匀的骰子,求出现1点的概率 | |
| C. | 在区间[1,4]上任取一数,求这个数大于1.5的概率 | |
| D. | 同时掷两枚质地均匀的骰子,求向上的点数之和是5的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
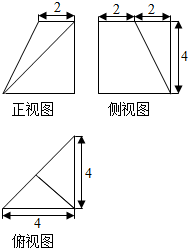
| A. | $\frac{16}{3}$ | B. | $\frac{80}{3}$ | C. | $\frac{40}{3}$ | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com