
已知函数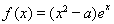 .
.
(Ⅰ)若函数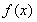 在
在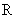 上不是单调函数,求实数
上不是单调函数,求实数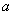 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数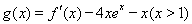 的零点个数.
的零点个数.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.
(1)分别求两次变换所对应的矩阵M1,M2.
(2)求△ABC在两次连续的变换作用下所得到的△A'B'C'的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:填空题
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 总计 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
总计 | 30 | 20 | 50 |
则在犯错误的概率不超过 的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:χ2=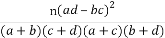
P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率.
(2)求该射手的总得分X的分布列.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
离散型随机变量X的概率分布规律为P(X=n)=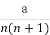 (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数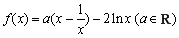 .
.
(Ⅰ)若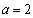 ,求曲线
,求曲线 在点
在点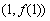 处的切线方程;
处的切线方程;
(Ⅱ)求函数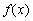 的单调区间;
的单调区间;
(Ⅲ)设函数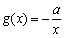 .若至少存在一个
.若至少存在一个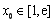 ,使得
,使得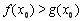 成立,求实数
成立,求实数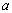 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数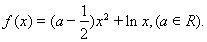
(Ⅰ)当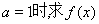 在区间
在区间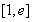 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间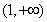 上,函数
上,函数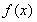 的图象恒在直线
的图象恒在直线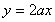 下方,求
下方,求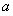 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com