
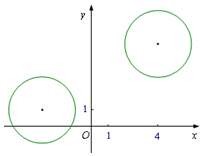
 在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.
在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.分析 (1)分类讨论,设方程,利用直线l1过点A(2,0),且与圆C1相切,建立方程求出斜率,即可求出直线l1的方程;
(2)设点P坐标为$(-\frac{3}{2},n)$,直线l1、l2的方程分别为:$y-n=k(x+\frac{3}{2})(k≠0),y-n=-\frac{1}{k}(x+\frac{3}{2})$,
即$kx-y+n+\frac{3}{2}k=0,x+ky-kn+\frac{3}{2}=0$,利用直线l3被圆C1截得的弦长与直线l4被圆C2截得的弦长相等,可得$\frac{{|-3k-1+n+\frac{3}{2}k|}}{{\sqrt{{k^2}+1}}}=\frac{{|4+5k-kn+\frac{3}{2}|}}{{\sqrt{{k^2}+1}}}$,化简利用关于k的方程有无穷多解,即可得出结论.
解答 解:(1)设直线l的方程为:y=k(x+1),即kx-y+k=0…(1分)
圆心C1到直线l的距离d=2,…(2分)
结合点到直线距离公式,得$\frac{|-3k-1+k|}{{\sqrt{{k^2}+1}}}=2$,…(3分)
求得$k=\frac{3}{4}$…(4分)
由于直线x=-1与圆C1相切.…(5分)
所以直线l的方程为:x=-1或$y=\frac{3}{4}(x+1)$,即x=-1或3x-4y+3=0…(6分)
(2)设点P坐标为$(-\frac{3}{2},n)$,直线l1、l2的方程分别为:$y-n=k(x+\frac{3}{2})(k≠0),y-n=-\frac{1}{k}(x+\frac{3}{2})$,
即$kx-y+n+\frac{3}{2}k=0,x+ky-kn+\frac{3}{2}=0$…(7分)
因为直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,两圆半径相等,
所以圆心C1到直线l1与圆心C2直线l2的距离相等.
故有$\frac{{|-3k-1+n+\frac{3}{2}k|}}{{\sqrt{{k^2}+1}}}=\frac{{|4+5k-kn+\frac{3}{2}|}}{{\sqrt{{k^2}+1}}}$,…(9分)
化简得$(\frac{7}{2}-n)k=-\frac{9}{2}-n,或(\frac{13}{2}-n)k=\frac{13}{2}-n$…(11分)
关于k的方程有无穷多解,有$n=\frac{13}{2}$
所以点P坐标为$(-\frac{3}{2},\frac{13}{2})$,经检验点$(-\frac{3}{2},\frac{13}{2})$满足题目条件.…(12分)
点评 本题是中档题,考查直线与圆的位置关系,对称的知识,注意方程无数解的条件,考查转化思想,函数与方程的思想,常考题型.


科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x<2} | B. | {x|0<x<2} | C. | {x|0<x≤1} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({3\sqrt{2},\frac{3π}{4}})$ | B. | $({3\sqrt{2},\frac{5π}{4}})$ | C. | $({3,\frac{5π}{4}})$ | D. | $({3,\frac{3π}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )
已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )| A. | $40+6\sqrt{3}$ | B. | $40+12\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{85}$ | D. | 85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 143 | B. | 144 | C. | 287 | D. | 288 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com