
分析 (1)利用点到直线距离公式,整理即可求得动点P的轨迹Γ;
(2)①将直线BF:y=-x-1,代入椭圆方程,即可求得B点坐标,利用直线的斜率公式即可求得直线l的方程;
②直线AB方程:y=kx+b,代入椭圆方程,由韦达定理,及∠OFA+∠OFB=180°,则kAF+kBF=0,即可求得b-2k=0,代入直线方程,即可求得直线l总经过点M(-2,0);
方法二:设直线AF方程:y=k(x+1),代入椭圆方程利用点斜式方程求得x=$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$=$\frac{2{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}}{{x}_{1}+{x}_{2}+2}$,利用韦达定理即可求得x=2,即可求得直线l总经过点M(-2,0).
解答 解:(1)设P(x,y),则$\frac{丨x+2丨}{\sqrt{(x+1)^{2}+{y}^{2}}}$=$\sqrt{2}$,
整理得:$\frac{{x}^{2}}{2}+{y}^{2}=1$,
∴动点P的轨迹Γ$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)①A(0,1),F(-1,0),则kAF=1,kBF=-1,直线BF:y=-x-1,
$\left\{\begin{array}{l}{y=-x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:3x2+4x=0,解得:x=0,x=-$\frac{4}{3}$,
代入y=-x-1,
解得:$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$(舍),$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=\frac{1}{3}}\end{array}\right.$,则B(-$\frac{4}{3}$,$\frac{1}{3}$),
kAB=$\frac{1-\frac{1}{3}}{0-(-\frac{4}{3})}$=$\frac{1}{2}$,
直线AB:y=$\frac{1}{2}$x+1,
②设方法一:A(x1,y1),B(x2,y2),直线AB方程:y=kx+b,
则$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,(k2+$\frac{1}{2}$)x2+2kbx+b2-1=0,
由韦达定理可知:x1+x2=-$\frac{2kb}{{k}^{2}+\frac{1}{2}}$,x1x2=$\frac{{b}^{2}-1}{{k}^{2}+\frac{1}{2}}$,
由∠OFA+∠OFB=180°,则kAF+kBF=$\frac{{y}_{1}}{{x}_{1}+1}$+$\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{k{x}_{1}+b}{{x}_{1}+1}$+$\frac{k{x}_{2}+b}{{x}_{2}+1}$=$\frac{(k{x}_{1}+b)({x}_{2}+1)+(k{x}_{2}+b)({x}_{1}+1)}{({x}_{1}+1)({x}_{2}+1)}$=0,
则2kx1x2+(k+b)(x1+x2)+2b=2k×$\frac{{b}^{2}-1}{{k}^{2}+\frac{1}{2}}$-(k+b)×$\frac{2kb}{{k}^{2}+\frac{1}{2}}$+2b=0,
则b-2k=0,
∴直线AB方程:y=k(x+2),直线l总经过点M(-2,0).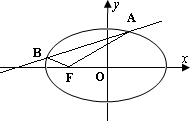
解法二:由于OFA+∠OFB=180°,则B关于x轴的对称点B1在直线AF上,
设A(x1,y1),B(x2,y2),B1(x2,-y2)
设直线AF方程:y=k(x+1),
代入$\frac{{x}^{2}}{2}+{y}^{2}=1$;得:
(k2+$\frac{1}{2}$)x2+2kx+k2-1=0,
由韦达定理可知:x1+x2=-$\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}$,x1x2=$\frac{{k}^{2}-1}{{k}^{2}+\frac{1}{2}}$,
则kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$,AB的方程为:y-y1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),令y=0,得:x=x1-y1×$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$,
y1=k(x1+1),-y2=k(x2+1),
x=$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$=$\frac{2{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}}{{x}_{1}+{x}_{2}+2}$=2,
∴直线l总经过定点M(-2,0).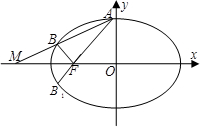
点评 本题考查直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,点斜式方程,考查计算能力,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
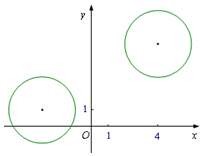 在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.
在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{10π}{3}$)的值为( )
函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{10π}{3}$)的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{3\sqrt{5}}{8}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论,其中正确的是( )
如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论,其中正确的是( )| A. | ① | B. | ③ | C. | ①③ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com