练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从2 012名学生中选取50名学生参加数学竞赛，若采用下面的方法选取：先用简单随机抽样从2 012人中剔除12人，剩下的2 000人再按系统抽样的方法抽取50人，则在2 012人中，每人入选的概率（ ）
    A.不全相等
    B.均不相等
    C.都相等，且为
    D.都相等，且为

    【答案】D
    【解析】解：根据题意，先用简单随机抽样的方法从2012人中剔除12人， 则剩下的再按系统抽样的抽取时，每人入选的概率为 = ，
    故每人入选的概率相等，
    故选：D．
    【考点精析】本题主要考查了系统抽样方法的相关知识点，需要掌握把总体的单位进行排序，再计算出抽样距离，然后按照这一固定的抽样距离抽取样本;第一个样本采用简单随机抽样的办法抽取才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对于实数x，符号[x]表示不超过x的最大整数，例如[π]=3，[﹣1.08]=﹣2，定义函数f（x）=x﹣[x]，下列命题中正确命题的序号 ．
    ①函数f（x）的最大值为1；
    ②函数f（x）的最小值为0；
    ③方程f（x）﹣ =0有无数个解；
    ④函数f（x）是增函数；
    ⑤对任意的x∈R，函数f（x）满足f（x+1）=f（x）；
    ⑥函数f（x）的图象与函数g（x）=|lgx|的图象的交点个数为10个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sinx的图象上所有点的横坐标缩短到原来的 倍（纵坐标不变），再将所得的图象向左平移 个单位长度后得到函数f（x）的图象
    （1）写出函数f（x）的解析式；
    （2）若对任意的x∈[﹣ ， ]，f2（x）﹣mf（x）﹣1≤0恒成立，求实数m的取值范围；
    （3）求实数a和正整数n，使得F（x）=f（x）﹣a在[0，nπ]上恰有2017个零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设向量 =（sinx， cosx）， =（﹣1，1）， =（1，1），其中x∈（0，π]．
    （1）若（ + ）∥ ，求实数x的值；
    （2）若 = ，求函数sinx的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 =（sinx，cosx）， =（sinx，k）， =（﹣2cosx，sinx﹣k）．
    （1）当x∈[0， ]时，求| + |的取值范围；
    （2）若g（x）=（ + ） ，求当k为何值时，g（x）的最小值为﹣ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按如图所示的程序框图操作： （Ⅰ）写出输出的数所组成的数集．若将输出的数按照输出的顺序从前往后依次排列，则得到数列{an}，请写出数列{an}的通项公式；
    （Ⅱ）如何变更A框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{2n}的前7项？
    （Ⅲ）如何变更B框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，平行六面体ABCD﹣A′B′C′D′，其中AB=4，AD=3，AA′=3，∠BAD=90°，∠BAA′=60°，∠DAA′=60°，则AC′的长为（ ）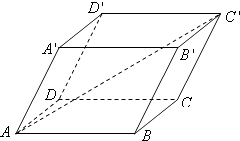
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知F1 ， F2是椭圆与双曲线的公共焦点，P是它们的一个公共点，且|PF1|＞|PF2|，椭圆的离心率为e1 ， 双曲线的离心率为e2 ， 若|PF2|=|F1F2|，则 + 的最小值为（ ）
    A.6+2
    B.8
    C.6+2
    D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】偶函数f（x）满足f（1﹣x）=f（1+x），且在x∈[0，1]时，f（x）= ，若直线kx﹣y+k=0（k＞0）与函数f（x）的图象有且仅有三个交点，则k的取值范围是 ．

    查看答案和解析>>

    同步练习册答案