
���� ��I�����ݼ�����ļ�������ó�ֱ�����꣮
��II�����|AB|��ֱ��AB�ķ��̣����P��ֱ��AB�������룬���������ε������ʽ�����������
��� �⣺��I��B��ļ�����Ϊ��2��$\frac{2��}{3}$����2cos$\frac{2��}{3}$=-1��2sin$\frac{2��}{3}$=$\sqrt{3}$��
��B��ֱ�����귽��Ϊ��-1��$\sqrt{3}$����
��II����A��ֱ�����귽��Ϊ��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����
��ֱ��AB�ķ���x+$\sqrt{3}$y-2=0��|AB|=$\sqrt{��\frac{1}{2}+1��^{2}+��\frac{\sqrt{3}}{2}-\sqrt{3}��^{2}}$=$\sqrt{3}$��
P��ֱ��AB�ľ���d=$\frac{|cos��+\sqrt{3}sin��-3|}{2}$=$\frac{|2sin����+\frac{��}{6}��-3|}{2}$��
�൱sin��$��+\frac{��}{6}$��=-1ʱ��dȡ�����ֵ$\frac{5}{2}$��
��S��ABP=$\frac{1}{2}|AB|•d$��$\frac{1}{2}��\sqrt{3}��\frac{5}{2}$=$\frac{5\sqrt{3}}{4}$��
���� ���⿼���˼�������ֱ�������ת�������빫ʽ��Ӧ�ã����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
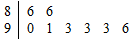 ��ͼ��ij��8λѧ��ʫ�ʱ����÷ֵľ�Ҷͼ����ô��8λѧ���÷ֵ���������λ���ֱ�Ϊ93��92��
��ͼ��ij��8λѧ��ʫ�ʱ����÷ֵľ�Ҷͼ����ô��8λѧ���÷ֵ���������λ���ֱ�Ϊ93��92���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=sin��2x-$\frac{��}{6}$�� | B�� | y=sin��x-$\frac{��}{6}$�� | C�� | y=cos��x-$\frac{��}{4}$�� | D�� | y=tan��2x+$\frac{��}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com