
分析 根据这种商品当天的市场价格与他的进货量(件)加上20成反比,这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元,求出比例系数,可得利润函数,再换元,利用基本不等式,即可得出结论.
解答 解:由题意,设市场价格y元,他的进货量为x件,则y=$\frac{k}{x+20}$,
∵这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元,
∴100=($\frac{k}{120}$-2)×100,∴k=360,
∴利润L=($\frac{360}{x+20}$-2)x,
设x+20=t(t≥20),则L=400-($\frac{7200}{t}$+2t)≤400-240=160,
当且仅当$\frac{7200}{t}$=2t,即t=60,x=40时,最大利润是160元.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,正确求出函数的解析式是关键.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | f($\sqrt{2}$)>f(-$\sqrt{2}$) | B. | f(-2)>f(3) | C. | f(3)<f(4) | D. | f($\sqrt{2}$)>f($\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
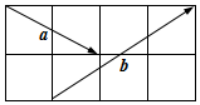 如图,在2×4的方格纸中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起点和终点均在格点的向量,则向量2$\overrightarrow a$+$\overrightarrow b$与$\overrightarrow a$-$\overrightarrow b$的夹角余弦值是$-\frac{{\sqrt{10}}}{10}$.
如图,在2×4的方格纸中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起点和终点均在格点的向量,则向量2$\overrightarrow a$+$\overrightarrow b$与$\overrightarrow a$-$\overrightarrow b$的夹角余弦值是$-\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com