
分析 (Ⅰ)若⊙F被l所截得的弦长为$2\sqrt{5}$,求出圆的半径,得到圆的方程,即可求|AB|;
(Ⅱ)求出P的坐标,即可判断直线PA与C的交点个数,
解答 解:(Ⅰ)抛物线C:y2=4x的焦点为F(1,0),
∵⊙F被l所截得的弦长为$2\sqrt{5}$,
∴圆的半径为$\sqrt{5+4}$=3,
∴⊙F的方程为(x-1)2+y2=9,
与y2=4x联立可得A(2,2$\sqrt{2}$),B(2,-2$\sqrt{2}$),∴|AB|=4$\sqrt{2}$;
(Ⅱ)(x-1)2+y2=9,令y=0,可得P(4,0),
∵A(2,2$\sqrt{2}$),∴直线PA与C的交点个数为2.
点评 本题考查圆的方程,考查抛物线的方程与性质,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
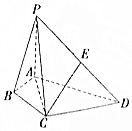 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
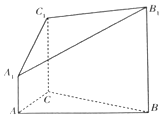 如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1
如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
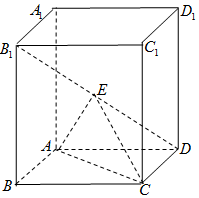 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{e})$ | B. | $(0,\frac{1}{2e})$ | C. | $[\frac{ln3}{3},\frac{1}{e})$ | D. | $[\frac{ln3}{3},1)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com