Question

【题目】已知函数f（x）=lnx﹣a2x2+ax，a∈R，且a≠0．
（1）若函数f（x）在区间[1，+∞）上是减函数，求实数a的取值范围；
（2）设函数g（x）=（3a+1）x﹣（a2+a）x2 ， 当x＞1时，f（x）＜g（x）恒成立，求a的取值范围．

Answer 1

【答案】
（1）解：∵f（x）=lnx﹣a2x2+ax，其定义域为（0，+∞），

∴f′（x）= ﹣2a2x+a= = ．

①当a=0时，f′（x）= ＞0，

∴f（x）在区间（0，+∞）上为增函数，不合题意．

②当a＞0时，f′（x）＜0（x＞0）等价于（2ax+1）（ax﹣1）＞0（x＞0），即x＞ ．

此时f（x）的单调递减区间为（ ，+∞）．

依题意，得 解之，得a≥1．

③当a＜0时，f′（x）＜0（x＞0）等价于（2ax+1）（ax﹣1）＞0（x＞0），即x＞﹣ ．

此时f（x）的单调递减区间为（﹣ ，+∞）．

依题意，得 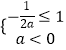解之，得a≤﹣ ．

综上所述，实数a的取值范围是（﹣∞，﹣ ]∪[1，+∞）

（2）解：∵g（x）=（3a+1）x﹣（a2+a）x2，

∴f（x）﹣g（x）=lnx﹣（2a+1）x+ax2＜0，

即lnx﹣x＜2ax﹣ax2，在（1，+∞）恒成立，

设h（x）=lnx﹣x，

则h′（x）= ﹣1＜0恒成立，

∴h（x）在（1，+∞）为减函数，

∴h（x）＜h（1）=﹣1，

∴ax2﹣2ax﹣1＜0，在（1，+∞）上恒成立，

设φ（x）=ax2﹣2ax﹣1

当a=0时，﹣1＜0，符合题意，

当a＞0时，显然不满足题意，

当a＜0，由于对称轴x=1，则φ（1）＜0，即a﹣2a﹣1＜0，解得﹣1＜a＜0，

综上所述，a的取值范围为（﹣1，0]

【解析】（1）先求导，再分类讨论，根据导数和函数的单调性的关系即可求出a的取值范围，（2）当x＞1时，f（x）＜g（x）恒成立，转化为lnx﹣x＜2ax﹣ax2 ， 在（1，+∞）恒成立，构造函数h（x）=lnx﹣x，利用导数求出函数最值，得到ax2﹣2ax﹣1＜0，在（1，+∞）上恒成立，再分类讨论，根据二次函数的性质即可求出a的取值范围．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．