
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �٣��������߶���Բ��ֻ���о���Բ��λ�ù�ϵ���ɣ�
�������жϣ����������ǹ���˫���ߣ���x���Ϸ��IJ��֣�����֪û�й����ߣ�
����֪Բ�������ߵġ��ڲ��������Բ����ܴ��ڹ����ߣ�
�������õ������C1�����ߣ�Ȼ���������C2�������б�ʽ��������⣮
��� �⣺����֪��C1�����ԣ�0��0��ΪԲ�ģ�r=2��Բ��C2�����ԣ�2��-1��ΪԲ�ģ�r=1��Բ��Բ�ľ�=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$�����ڰ뾶֮��1��С�ڰ뾶֮��3������Բ�ཻ���������������ߣ��ʢ���ȷ��
����֪������C1��C2�ǹ���˫���ߣ����Ǹ�����x���Ϸ��IJ��֣������������û�й����ߣ��ʢڴ���
����Ϊb��a��0��������ͬһ����ϵ���������ǵ�ͼ�����£�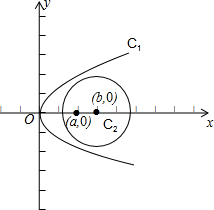
���������߲����й����ߣ��ʢ���ȷ��
�ܵ�a=1ʱ��C1��y=lnx�������x=1ʱ�����߷���Ϊy=x-1������C2����x=1ʱ�����߷���2Ϊy=x-1���ʢ���ȷ��
����������������ȷ��
��ѡ��C��
���� ���⿼����Բ���ߵı����̼������ʡ����߷��̵���ͬʱ����Ϊ�¶������⣬Ҫע��ԡ���������⣮


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-2y-13=0 | B�� | 3x-2y-13=0��x-2y-3=0 | ||
| C�� | x-2y-3=0 | D�� | x-2y-3=0��2x+3y-13=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$��1-$\frac{1}{e}$�� | B�� | $\frac{1}{4}$��1-$\frac{1}{e}$�� | C�� | $\frac{1}{e}$ | D�� | 1-$\frac{1}{e}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{��-1}{4}$ | D�� | $\frac{��-2}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$��4 | B�� | 0��4 | C�� | -$\frac{1}{4}$��2 | D�� | 0��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼĦ���ְ뾶10�ף���͵�A�����0.5�ף���֪Ħ���ְ���ʱ�뷽��ÿ3����תһȦ�����ʾ��ȣ����˴���͵�A��ȥ�ҿ�ʼ��ʱ����t�ַ��Ӻ������10sin��$\frac{2}{3}��$t$-\frac{��}{2}$��+10.5��10.5-10cos��$\frac{2}{3}$��t���ף�
��ͼĦ���ְ뾶10�ף���͵�A�����0.5�ף���֪Ħ���ְ���ʱ�뷽��ÿ3����תһȦ�����ʾ��ȣ����˴���͵�A��ȥ�ҿ�ʼ��ʱ����t�ַ��Ӻ������10sin��$\frac{2}{3}��$t$-\frac{��}{2}$��+10.5��10.5-10cos��$\frac{2}{3}$��t���ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com