Question

17．已知区域Ω={（x，y）|$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$，区域A={（x，y）|0≤y≤$\frac{1}{2}$e^-|x|，x∈[-1，1]，在Ω内随机投掷一点M，则点M落在区域A内的概率是（　　）

• A． $\frac{1}{2}$（1-$\frac{1}{e}$）
• B． $\frac{1}{4}$（1-$\frac{1}{e}$）
• C． $\frac{1}{e}$
• D． 1-$\frac{1}{e}$

Answer 1

分析 本题符合几何概型，所以只要分别求出两个区域的面积，利用面积比求概率．

解答 解：由题意，两个区域对应的图形如下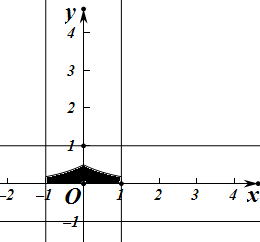，区域Ω是图中边长为2的正方形，区域A是阴影部分，面积为${2∫}_{0}^{1}\frac{1}{2}{e}^{-x}dx$=2（$-\frac{1}{2}{e}^{-x}$）${\;}_{0}^{1}$=1-$\frac{1}{e}$，
由几何概型公式可得点M落在区域A内的概率是$\frac{1-\frac{1}{e}}{2×2}=\frac{1}{4}（1-\frac{1}{e}）$；
故选B．

点评 本题考查了利用定积分求曲边梯形的面积以及几何概型公式的运用；关键是求出区域A的面积，利用几何概型公式解答．