
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,单调减区间是
时,单调减区间是![]() ,单调增区间是
,单调增区间是![]() ,
,![]() ;当
;当![]() 时,单调增区间是
时,单调增区间是![]() ,没有单调减区间;(2)
,没有单调减区间;(2)![]() .
.
【解析】
(1)先求函数的定义域,利用函数的导函数![]() ,得
,得![]() 或
或![]() ,当
,当![]() 时,分
时,分![]() ,
,![]() 讨论即可得到答案;
讨论即可得到答案;
(2)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由题意得
,由题意得![]() ,即
,即![]() ,令
,令![]() ,求新函数
,求新函数![]() 的最大值即可得实数
的最大值即可得实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ;
;
当![]() 即
即![]() 时,当
时,当![]() 时都有
时都有![]() ;
;
![]() 当
当![]() 时,单调减区间是
时,单调减区间是![]() ,单调增区间是
,单调增区间是![]() ,
,![]() ;
;
当![]() 时,单调增区间是
时,单调增区间是![]() ,没有单调减区间.
,没有单调减区间.
(2)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
对任意![]() ,存在
,存在![]() ,使得
,使得![]() ,
,
即存在![]() ,使
,使![]() 的值不超过
的值不超过![]() 在区间
在区间![]() 上的最小值
上的最小值![]() .
.
由![]() ,
,![]() .
.
令![]() ,则当
,则当![]() 时,
时,![]() .
.
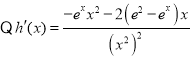
![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时,
时,![]()
![]() ,
,![]() .
.
故![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,
,
从而![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知对于任意![]() ,函数
,函数![]()
![]() 与
与![]()
![]() 的图像在
的图像在![]() 上都有三个不同交点.
上都有三个不同交点.
(1)写出![]() 的解析式,并求函数的最大值及此时的x的取值;
的解析式,并求函数的最大值及此时的x的取值;
(2)若函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,且
上单调递减,且![]() ,求
,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高(不超过三次)的多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即:![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
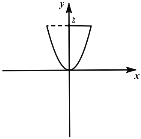
,![]() 依次为几何体的高,下底面积,上底面积,中截面面积.如图,现将曲线
依次为几何体的高,下底面积,上底面积,中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体.利用辛卜生公式可求得该几何体的体积
轴旋转一周得到一个几何体.利用辛卜生公式可求得该几何体的体积![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的一点
上的一点![]() 到其左顶点
到其左顶点![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(
两点(![]() 与点
与点![]() 不重合),若以
不重合),若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,试证明:直线
,试证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 及
及![]() ;
;
(2)若![]() 且数列
且数列![]() 为周期函数,且最小正周期
为周期函数,且最小正周期![]() ,求
,求![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 成等比数列?若存在,求出所有这样的
成等比数列?若存在,求出所有这样的![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿水青山就是金山银山.近年来,祖国各地依托本地自然资源,打造旅游产业,旅游业正蓬勃发展.景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念,合力使旅游市场走上规范有序且可持续的发展轨道.某景区有一个自愿消费的项目:在参观某特色景点入口处会为每位游客拍一张与景点的合影,参观后,在景点出口处会将刚拍下的照片打印出来,游客可自由选择是否带走照片,若带走照片则需支付20元,没有被带走的照片会收集起来统一销毁.该项目运营一段吋间后,统计出平均只有三成的游客会选择带走照片,为改善运营状况,该项目组就照片收费与游客消费意愿关系作了市场调研,发现收费与消费意愿有较强的线性相关性,并统计出在原有的基础上,价格每下调1元,游客选择带走照片的可能性平均增加0.05,假设平均每天约有5000人参观该特色景点,每张照片的综合成本为5元,假设每个游客是否购买照片相互独立.
(1)若调整为支付10元就可带走照片,该项目每天的平均利润比调整前多还是少?
(2)要使每天的平均利润达到最大值,应如何定价?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列A:![]() ,
,![]() ,…
,…![]() (
(![]() ).如果对小于
).如果对小于![]() (
(![]() )的每个正整数
)的每个正整数![]() 都有
都有![]() <
<![]() ,则称
,则称![]() 是数列A的一个“G时刻”.记“
是数列A的一个“G时刻”.记“![]() 是数列A的所有“G时刻”组成的集合.
是数列A的所有“G时刻”组成的集合.
(1)对数列A:-2,2,-1,1,3,写出![]() 的所有元素;
的所有元素;
(2)证明:若数列A中存在![]() 使得
使得![]() >
>![]() ,则
,则![]() ;
;
(3)证明:若数列A满足![]() -
-![]() ≤1(n=2,3, …,N),则
≤1(n=2,3, …,N),则![]() 的元素个数不小于
的元素个数不小于![]() -
-![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com