
分析 (1)利用奇函数的性质,可得f(0)=0,由此求得a的值.
(2)根据函数的导数区间(1,+∞)上小于零,可得f(x)在区间(1,+∞)上单调递减.
(3)利用函数f(x)在(1,+∞)上是减函数,且x2-x+2>1,f(x2-x+2)<f(4),可得x2-x+2>4,由此求得不等式的解集.
解答 解:(1)∵函数f(x)=$\frac{x+a}{{x}^{2}+1}$是奇函数,故有f(0)=$\frac{a}{1}$=0,∴a=0.
(2)证明:∵y=f(x)=$\frac{x}{{x}^{2}+1}$,∴f′(x)=$\frac{1{-x}^{2}}{{{(x}^{2}+1)}^{2}}$,
∵当x>1时,f′(x)<0,
∴f(x)在区间(1,+∞)上单调递减.
(3)由′(x)=$\frac{1{-x}^{2}}{{{(x}^{2}+1)}^{2}}$,
可得函数f(x)的增区间为(-1,1),减区间为(1,+∞)、(-∞,-1)
∵x2-x+2=${(x-\frac{1}{2})}^{2}$+$\frac{π}{4}$≥$\frac{7}{4}$,
故由不等式f(x2-x+2)<f(4),可得x2-x+2>4,求得x<-1,或x>2,
故不等式的解集为{x|x<-1,或 x>2}.
点评 本题主要考查奇函数的性质,函数的导数与函数的单调性的关系,利用函数的单调性解不等式,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
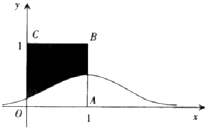 设随机变量X~N(1,σ2),其正态分布密度曲线如图所示,且P(-1<X≤3)=0.9544,那么向正方形OABC中随机投掷20000个点,则落入阴影部分的点的个数的估计值为( )
设随机变量X~N(1,σ2),其正态分布密度曲线如图所示,且P(-1<X≤3)=0.9544,那么向正方形OABC中随机投掷20000个点,则落入阴影部分的点的个数的估计值为( )| A. | 15078 | B. | 14056 | C. | 13174 | D. | 12076 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $-\frac{{\sqrt{6}+\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P1<P2 | B. | P1>P2 | C. | P1=P2 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com