Question

19．机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心出发，先沿北偏西θ（sinθ=$\frac{12}{13}$）方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B，C都在圆上，则在以线段BC中点为坐标原点O，正东方向为x轴正方向，正北方向为y轴正方向的直角坐标系中，圆的标准方程为x²+（y-9）²=225．

Answer 1

分析 由已知求解三角形得OT、BT的长度，以BC所在直线为x轴，以BC得垂直平分线为y轴距离平面直角坐标系，可得圆T的圆心坐标，代入圆的标准方程得答案．

解答 解：如图所示：sinθ=$\frac{12}{13}$，TA=13，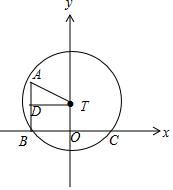
∴cos∠ATD=sinθ=$\frac{12}{13}$，TD=TA•cos∠ATD=13×$\frac{12}{13}$=12，
AD=TA•sin∠ATD=13×$\frac{5}{13}$=5，
∴BD=14-AD=9，∴TB²=TD²+BD²=144+81=225，
以BC所在直线为x轴，以BC得垂直平分线为y轴距离平面直角坐标系，
则T（0，9），
故圆T的方程为 x²+（y-9）²=225，
故答案为：x²+（y-9）²=225．

点评 本题主要考查直角三角形中的边角关系，求圆的标准方程，体现了数形结合的数学思想，属于中档题．