
分析 利用三角函数的诱导公式,得出sin(α+$\frac{7π}{6}$)=…=-cos(α-$\frac{π}{3}$),再求cos(α+$\frac{7π}{6}$)的值.
解答 解:∵sin(α+$\frac{7π}{6}$)=-sin(α+$\frac{π}{6}$)
=-sin(α-$\frac{π}{3}$+$\frac{π}{2}$)
=-cos(α-$\frac{π}{3}$)
=-$\frac{4}{5}$,
∴cos(α+$\frac{7π}{6}$)=±$\frac{3}{5}$.
故答案为:±$\frac{3}{5}$.
点评 本题考查了三角函数的诱导公式与求值问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 顾客人数/商品 | 甲 | 乙 | 丙 | 丁 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
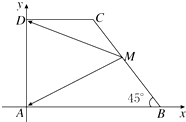 在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )
在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1+\frac{1}{{2}^{n}}$ | B. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n}}$ | ||
| C. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$+$\frac{1}{{2}^{n-1}}$ | D. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 容量,方差 | B. | 容量,平均数 | C. | 平均数,容量 | D. | 标准差,平均数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com