
| A. | (X∪Y)○Z=(X○Z)∩(Y○Z) | B. | (X∩Y)○Z=(X○Z)∪(Y○Z) | C. | (X∪Y)○Z=(X○Z)∪(Y○Z) | D. | (X∩Y)○Z=(X○Z)∩(Y○Z) |
分析 利用集合的运算性质、复合函数的图象与性质即可判断出结论.
解答 解:?X,Y,Z⊆I,不妨取X={(x,y)|y=x,x,y∈R},Y={(y,z)z=y2,z∈R,y∈X},Z={(z,t)|t=2z,z∈Y,t∈R},
对于:X∪Y={(x,y)|y=x,y=x2},X∩Y={(0,0),(1,1)},
∴(X∪Y)○Z={(x,y)|$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}}\end{array}\right.$或$\left\{\begin{array}{l}{y=x}\\{y=2{x}^{2}}\end{array}\right.$}={(0,0),(1,1),$(\frac{1}{2},\frac{1}{2})$}.
((X∩Y)○Z={(0,0)};
(X○Z)={(0,0)},(Y○Z)={(0,0)}
只有B满足.
故选:B.
点评 本题考查了集合的运算性质、复合函数的图象与性质,考查了数形结合方法、推理能力与计算能力,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,1-2$\sqrt{2}$] | B. | (-∞,1-2$\sqrt{2}$] | C. | [1+2$\sqrt{2}$,+∞) | D. | [1+2$\sqrt{2}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
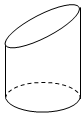 用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.
用一个不平行于底面的平面截一个底面直径为6cm的圆柱,得到如图几何体,若截面椭圆的长轴长为10cm,这个几何体最短的母线长为6cm,则此几何体的体积为90πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个单位长度 | B. | 向右平移1个单位长度 | ||
| C. | 向左平移$\frac{1}{3}$个单位长度 | D. | 向右平移$\frac{1}{3}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com