
| A. | (-2,1-2$\sqrt{2}$] | B. | (-∞,1-2$\sqrt{2}$] | C. | [1+2$\sqrt{2}$,+∞) | D. | [1+2$\sqrt{2}$,4] |
分析 根据条件可得到a<-1,$\frac{1}{a}+\frac{a}{b}<0$,且$b=\frac{1-a}{2}$,带入$\frac{1}{a}+\frac{a}{b}$并整理可得$\frac{1}{a}+\frac{a}{b}=\frac{2{a}^{2}-a+1}{a-{a}^{2}}$,可设$\frac{2{a}^{2}-a+1}{a-{a}^{2}}=m$,可整理成关于a的方程的形式为(2+m)a2-(1+m)a+1=0,并得出该方程为关于a的一元二次方程,并在(-∞,-1)上有解,可设f(a)=(2+m)a2-(1+m)a+1,这样可由m<0,f(-1)及判别式△的取值即可得出$m≤1-\sqrt{2}$.而根据条件可以得出$\frac{1}{a}+\frac{a}{b}=\frac{1}{a}+\frac{1}{b}-2$,从而得出m一定满足m>-3,这样根据选项便可找出正确选项.
解答 解:由a+2b=1得,$b=\frac{1-a}{2}$①;
∵b>1;
∴$\frac{1-a}{2}>1$;
∴a<-1;
∴$\frac{1}{a}+\frac{a}{b}<0$;
将①带入$\frac{1}{a}+\frac{a}{b}$得:$\frac{1}{a}+\frac{a}{b}=\frac{1}{a}+\frac{2a}{1-a}=\frac{2{a}^{2}-a+1}{a-{a}^{2}}$;
设$\frac{2{a}^{2}-a+1}{a-{a}^{2}}=m$,整理成关于a的方程为:(2+m)a2-(1+m)a+1=0②,该方程在(-∞,-1)上有解;
若m=-2,a=-1,不符合a<-1;
∴m≠-2;
∴方程②为关于a的一元二次方程,在(-∞,-1)上有解;
设f(a)=(2+m)a2-(1+m)a+1,则a应满足:
f(-1)=2m+4<0(1),或$\left\{\begin{array}{l}{△={m}^{2}-2y-7>0}\\{2m+4≥0}\end{array}\right.$(2),或$\left\{\begin{array}{l}{△={m}^{2}-2y-7=0}\\{f(-1)=2m+4>0}\end{array}\right.$(3);
解(1)得,m<-2,解(2)得,$-2≤m<1-2\sqrt{2}$,或$m>1+2\sqrt{2}$,解(3)得,$m=1-2\sqrt{2}$;
又m<0;
∴m$≤1-2\sqrt{2}$;
由a+2b=1得,$\frac{a}{b}+2=\frac{1}{b}$;
∴$\frac{a}{b}=\frac{1}{b}-2$;
∴$\frac{1}{a}+\frac{a}{b}=\frac{1}{a}+\frac{1}{b}-2$;
∵a<-1,b>1;
∴$\frac{1}{a}>-1,0<\frac{1}{b}<1$;
∴一定有$\frac{1}{a}+\frac{1}{b}-2>-3$成立,及m>-3;
m一定满足$-3<m≤1-2\sqrt{2}$;
即$-3<\frac{1}{a}+\frac{a}{b}≤1-2\sqrt{2}$;
∴只有选项A正确.
故选:A.
点评 考查不等式的性质,以及通过将函数解析式变成关于自变量的方程的形式,然后根据方程在自变量所在区间上有解来求函数值域的方法,一元二次方程的解的情况和判别式△取值的关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
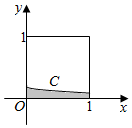 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-2,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(-2,1)的密度曲线)的点的个数的估计值为( )| A. | 430 | B. | 215 | C. | 2718 | D. | 1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (X∪Y)○Z=(X○Z)∩(Y○Z) | B. | (X∩Y)○Z=(X○Z)∪(Y○Z) | C. | (X∪Y)○Z=(X○Z)∪(Y○Z) | D. | (X∩Y)○Z=(X○Z)∩(Y○Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com