
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ex |
| x |
| ex |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| ex |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| ex |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| ex(x-1) |
| x2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| e |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| e |
| e |


科目:高中数学 来源: 题型:
| A、三角形的内角是第一象限角或第二象限角 | ||
| B、第一象限角是锐角 | ||
| C、第一象限角不是锐角 | ||
D、角α是第四象限角则有2kπ-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
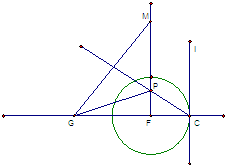 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知| |PF| |
| d |
| ||
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| GF |
| FC |
| MP |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:

| A、31次 | B、32次 |
| C、33次 | D、35次 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为| π |
| 3 |
| PM |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:
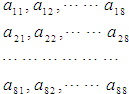 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=| 1 |
| 2 |
| 1 |
| 4 |
| 36 |
| An |
| bn |
| an |
| c | 2 1 |
| c | 2 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
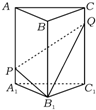 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com