
分析 (Ⅰ)求出导数,求得切线的斜率和切点,由切线方程,可得a,b的方程,解方程可得a,b的值;
(Ⅱ)由题意可得$\frac{x}{1+{e}^{x}}$+e-x>$\frac{x}{{e}^{x}-1}$+ke-x,即有(1-k)e-x>$\frac{2x}{{e}^{2x}-1}$,即1-k>$\frac{2x}{{e}^{x}-{e}^{-x}}$,可令g(x)=$\frac{2x}{{e}^{x}-{e}^{-x}}$,求出导数,判断单调性,可得最值,即可得到k的范围.
解答 解:(Ⅰ)f(x)=$\frac{ax}{{e}^{x}+1}$+be-x的导数为
f′(x)=$\frac{a({e}^{x}+1)-ax{e}^{x}}{({e}^{x}+1)^{2}}$,
由切线方程为x+2y-2=0,可得
f(0)=1,f′(0)=-$\frac{1}{2}$,
即有b=1,$\frac{1}{2}$a-b=-$\frac{1}{2}$,
解得a=b=1;
(Ⅱ)当x≠0时,都有f(x)>$\frac{x}{{e}^{x}-1}$+ke-x,即为
$\frac{x}{1+{e}^{x}}$+e-x>$\frac{x}{{e}^{x}-1}$+ke-x,
即有(1-k)e-x>$\frac{2x}{{e}^{2x}-1}$,即1-k>$\frac{2x}{{e}^{x}-{e}^{-x}}$,
可令g(x)=$\frac{2x}{{e}^{x}-{e}^{-x}}$,g(-x)=$\frac{-2x}{{e}^{-x}-{e}^{x}}$=g(x),
即有g(x)为偶函数,只要考虑x>0的情况.
由g(x)-1=$\frac{2x-{e}^{x}+{e}^{-x}}{{e}^{x}-{e}^{-x}}$,
x>0时,ex>e-x,
由h(x)=2x-ex+e-x,h′(x)=2-(ex+e-x)≤2-2$\sqrt{{e}^{x}•{e}^{-x}}$=0,
则h(x)在x>0递减,即有h(x)<h(0)=0,
即有g(x)<1.
故1-k≥1,解得k≤0.
则k的取值范围为(-∞,0].
点评 本题考查导数的运用:求切线的斜率和单调性,考查不等式恒成立问题的解法,注意运用参数分离和构造函数,求出导数,判断单调性,求出最值,考查运算能力,属于中档题.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
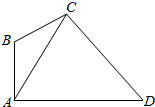 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若a=1,则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若非p是q的必要条件,则p是非q的充分条件 | |
| B. | “x>2”是“$\frac{1}{x}<\frac{1}{2}$”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x≥0”的否定是“?x∈R,x2-x<0” | |
| D. | 若p且q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com