
分析 (1)设等差数列{an}公差为d>0,由a2=4,a4+a6=20可求得公差为d及数列{an}的通项公式;
(2)由(1)知an=2n,由裂项法得$\frac{4}{{a}_{n}{a}_{n+1}}$=4×$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$)=($\frac{1}{n}$-$\frac{1}{n+1}$),从而可求得数列$\left\{{\frac{4}{{{a_n}{a_{n+1}}}}}\right\}$的前n项和Sn.
解答 解:(1)设等差数列{an}公差为d,则d>0,
∵a4+a6=2a5=20,
∴a5=10,又a2=4,
∴d=$\frac{{a}_{5}{-a}_{2}}{5-2}$=2,
∴an=a2+(n-2)d=4+2(n-2)=2n;
(2)∵$\frac{4}{{a}_{n}{a}_{n+1}}$=$\frac{4}{2n(2n+2)}$=$\frac{1}{n(n+1)}$=($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Sn=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查数列的求和,突出考查裂项法的应用,求得数列{an}的通项公式是关键,属于中档题.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,1)∪(2,+∞) | B. | [0,1]∪(2,+∞) | C. | [0,1] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
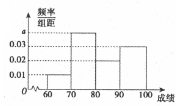 在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1,1 | B. | $-\frac{3}{2},-1$ | C. | $-\frac{3}{2},3$ | D. | $-2,\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com