【题目】已知函数f（x）=2sin（x+ 
）cosx．
（1）若0≤x≤ 
，求函数f（x）的值域；
（2）设△ABC的三个内角A，B，C所对的边分别为a，b，c，若A为锐角且f（A）= 
，b=2，c=3，求cos（A﹣B）的值．
【答案】
（1）解：f（x）=2sin（x+ 
）cosx
=（sinx+ 
cosx）cosx
=sinxcosx+ cos2x
= 
sin2x+ 
cos2x+
=sin（2x+ ）+ ；
由 
得， 
，
∴ 
，
∴ 
，
即函数f（x）的值域为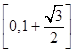 
（2）解：由 
，
得 
，
又由 
，∴ 
，
∴ 
，解得 
；
在△ABC中，由余弦定理a2=b2+c2﹣2bccosA=7，
解得 
；
由正弦定理 
，得 
，
∵b＜a，∴B＜A，∴ 
，
∴cos（A﹣B）=cosAcosB+sinAsinB
= 
【解析】（1）利用三角恒等变换化简f（x），根据x的取值范围即可求出函数f（x）的值域；（2）由f（A）的值求出角A的大小，再利用余弦定理和正弦定理，即可求出cos（A﹣B）的值．
科目：高中数学 来源： 题型：
【题目】已知函数y=f（x）的导函数y=f'（x）的图象如图所示，给出如下命题：
①0是函数y=f（x）的一个极值点；
②函数y=f（x）在 
处切线的斜率小于零；
③f（﹣1）＜f（0）；
④当﹣2＜x＜0时，f（x）＞0．
其中正确的命题是 ． （写出所有正确命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数 
，其中a∈R．
（1）根据a的不同取值，讨论f（x）的奇偶性，并说明理由；
（2）已知a＞0，函数f（x）的反函数为f﹣1（x），若函数y=f（x）+f﹣1（x）在区间[1，2]上的最小值为1+log23，求函数f（x）在区间[1，2]上的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等差数列{an}的公差d≠0满足
成等比数列，若
=1，Sn是{
}的前n项和，则
的最小值为________．
【答案】4
【解析】
成等比数列，=1，可得：
= 
，即（1+2d）2=1+12d，d≠0，解得d．可得an，Sn．代入利用分离常数法化简后，利用基本不等式求出式子的最小值．
∵成等比数列，a1=1，
∴= ，
∴（1+2d）2=1+12d，d≠0，
解得d=2．
∴an=1+2（n﹣1）=2n﹣1．
Sn=n+
×2=n2．
∴=
=n+1+
﹣2≥2
﹣2=4，
当且仅当n+1=时取等号，此时n=2，且取到最小值4，
故答案为：4．
【点睛】
本题考查了等差数列的通项公式、前n项和公式，等比中项的性质，基本不等式求最值，在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.
【题型】填空题
【结束】
17
【题目】设
是公比为正数的等比数列,
,
(1)求的通项公式;
(2)设
是首项为1,公差为2的等差数列,求数列
的前
项和
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知公差不为0的等差数列{an}中，a1=2，且a2+1，a4+1，a8+1成等比数列．
（1）求数列{an}通项公式；
（2）设数列{bn}满足bn= 
，求适合方程b1b2+b2b3+…+bnbn+1= 
的正整数n的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
