【题目】若函数f（x）=|x﹣1|+m|x﹣2|+6|x﹣3|在x=2时取得最小值，则实数m的取值范围是 ．
【答案】[5，+∞）
【解析】解：当x＜1时，f（x）=1﹣x+2m﹣mx+18﹣6x=19+2m﹣（m+7）x，当1≤x＜2时，f（x）=x﹣1+2m﹣m，x+18﹣6x=17+2m﹣（m+5）x，f（1）=12+m，
2≤x＜3时，f（x）=x﹣1+mx﹣2m+18﹣6x=17﹣2m+（m﹣5）x，f（2）=7，
当x≥3时，f（x）=x﹣1+mz﹣2m+6x﹣18=﹣19﹣2m+（m+7）x，f（3）=m+2，
若函数f（x）=|x﹣1|+m|x﹣2|+6|x﹣3|在x=2时取得最小值，
则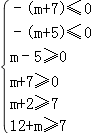 
解得m≥5，
故m的取值范围为[5，+∞），
所以答案是：[5，+∞），
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．
科目：高中数学 来源： 题型：
【题目】数列{an}中，Sn是{an}的前n项和且Sn=2n﹣an ，
（1）求a1 ， an；
（2）若数列{bn}中，bn=n（2﹣n）（an﹣2），且对任意正整数n，都有 
，求t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四个命题中正确的是______．
①已知定义在R上的偶函数
，则
；
②若函数
，
，值域为
，且存在反函数，则函数，与函数
，
是两个不同的函数﹔
③已知函数
，既无最大值，也无最小值；
④函数
的所有零点构成的集合共有4个子集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|2x﹣1|+a|x﹣1|
（I）当a=1时，解关于x的不等式f（x）≥4
（II）若f（x）≥|x﹣2|的解集包含[ 
，2]，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边长分别为a，b，c，且cos 
．
（1）若a=3，b= 
，求c的值；
（2）若f（A）=sinA（ 
cosA﹣sinA），求f（A）的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，a，b∈R，a≠0，b≠0，f（1）= 
，且方程f（x）=x有且仅有一个实数解；
（1）求a、b的值；
（2）当x∈（ 
， ]时，不等式（x+1）f（x）＞m（m﹣x）﹣1恒成立，求实数m的范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=2sin（x+ 
）cosx．
（1）若0≤x≤ 
，求函数f（x）的值域；
（2）设△ABC的三个内角A，B，C所对的边分别为a，b，c，若A为锐角且f（A）= 
，b=2，c=3，求cos（A﹣B）的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
