练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四面体的所有顶点在球的表面上，平面，，，则球的表面积为_________.

    【答案】

    【解析】

    将四面体补成直三棱柱，根据题意画出图象，设，的外心分别为，，则点为线段的中点，求出，在根据正弦定理，求出，根据勾股定理和球的表面积公式，即可求得答案.

    四面体的所有顶点在球的表面上，且平面，

    将四面体补成直三棱柱，

    设，的外心分别为，，则点为线段的中点，

    根据直棱柱特征可得：面

    根据题意画出图象，如图：

    [Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565330432/EXPLANATION/6f612c2d35a74b139ecb71f4a35bdeaa.png]

    可得：，

    在根据正弦定理：(为三角形外接圆半径)

    根据为的外心，可得为外接圆半径

    即，

    面，面

    故为直角三角形

    在中，根据勾股定理可得：，

    .

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数－2为自然对数的底数，)．

    (1)若曲线在点处的切线与曲线至多有一个公共点时，求的取值范围；

    (2)当时，若函数有两个零点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）讨论函数零点的个数；

    （2）若函数存在两个零点，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

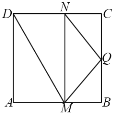
    【题目】如图，在边长等于2正方形中，点Q是中点，点M，N分别在线段上移动（M不与A，B重合，N不与C，D重合），且，沿着将四边形折起，使得面面，则三棱锥体积的最大值为________；当三棱锥体积最大时，其外接球的表面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，点在轴上，点在轴上，且，，当点在轴上运动时，动点的轨迹为曲线.过轴上一点的直线交曲线于，两点.

    （1）求曲线的轨迹方程；

    （2）证明：存在唯一的一点，使得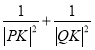为常数，并确定点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人，这里的“六艺”其实源于中国周朝的贵族教育体系，具体包括“礼、乐、射、御、书、数”. 为弘扬中国传统文化，某校在周末学生业余兴趣活动中开展了“六艺”知识讲座，每艺安排一节，连排六节，则满足“数”必须排在前两节，“礼”和“乐”必须相邻安排的概率为( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy上取两个定点A1（，0），A2（，0），再取两个动点N1（0，m），N2（0，n），且mn＝2.

    （1）求直线A1N1与A2N2交点M的轨迹C的方程；

    （2）过R（3，0）的直线与轨迹C交于P，Q，过P作PN⊥x轴且与轨迹C交于另一点N，F为轨迹C的右焦点，若（λ＞1），求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左顶点为A，O为坐标原点，，C的离心率为．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）已知不经过点A的直线交椭圆C于M，N两点，线段MN的中点为B，若，求证：直线l过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中k∈R.

    （1）当时，求函数的单调区间；

    （2）当k∈[1，2]时，求函数在[0，k]上的最大值的表达式，并求的最大值.

    查看答案和解析>>

    同步练习册答案