
【题目】在直角坐标系xOy上取两个定点A1(![]() ,0),A2(
,0),A2(![]() ,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
,0),再取两个动点N1(0,m),N2(0,n),且mn=2.
(1)求直线A1N1与A2N2交点M的轨迹C的方程;
(2)过R(3,0)的直线与轨迹C交于P,Q,过P作PN⊥x轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() (λ>1),求证:
(λ>1),求证:![]() .
.
【答案】(1)![]() 1(x≠±
1(x≠±![]() );(2)证明见解析
);(2)证明见解析
【解析】
(1)根据题意先写出两直线的方程,再根据条件化简即可求得答案;
(2)设P(x1,y1),Q(x2,y2),设l:x=ty+3,联立直线与椭圆的方程,由韦达定理得y1+y2![]() 且y1y2
且y1y2![]() ,根据题意得 x1﹣3=λ(x2﹣3),y1=λy2,再代入即可证明结论.
,根据题意得 x1﹣3=λ(x2﹣3),y1=λy2,再代入即可证明结论.
(1)解:依题意知直线A1N1的方程为:y![]() (x
(x![]() )…①;
)…①;
直线A2N2的方程为:y![]() (x
(x![]() )…②
)…②
设Q(x,y)是直线A1N1与A2N2交点,①、②相乘,得y2![]() (x2﹣6)
(x2﹣6)
由mn=2整理得:![]() 1
1
∵N1、N2不与原点重合,可得点A1,A2不在轨迹M上,
∴轨迹C的方程为![]() 1(x≠±
1(x≠±![]() );
);
(2)证明:设l:x=ty+3,代入椭圆方程消去x,得(3+t2)y2+6ty+3=0.
设P(x1,y1),Q(x2,y2),N(x1,﹣y1),可得y1+y2![]() 且y1y2
且y1y2![]() ,
,
![]() ,可得(x1﹣3,y1)=λ(x2﹣3,y2),∴x1﹣3=λ(x2﹣3),y1=λy2,
,可得(x1﹣3,y1)=λ(x2﹣3,y2),∴x1﹣3=λ(x2﹣3),y1=λy2,
证明![]() ,只要证明(2﹣x1,y1)=λ(x2﹣2,y2),∴2﹣x1=λ(x2﹣2),
,只要证明(2﹣x1,y1)=λ(x2﹣2,y2),∴2﹣x1=λ(x2﹣2),
只要证明![]() ,只要证明2t2y1y2+t(y1+y2)=0,
,只要证明2t2y1y2+t(y1+y2)=0,
由y1+y2![]() 且y1y2
且y1y2![]() ,代入可得2t2y1y2+t(y1+y2)=0,
,代入可得2t2y1y2+t(y1+y2)=0,
∴![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为1的等差数列,
是公差为1的等差数列,![]() 是单调递增的等比数列,且
是单调递增的等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ;
;
(3)若数列![]() 的前
的前![]() 项积为
项积为![]() ,求
,求![]() .
.
(4)数列![]() 满足
满足![]() ,
,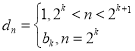 ,其中
,其中![]() ,
,![]() ,求
,求![]() .
.
(5)解决数列问题时,经常需要先研究陌生的通项公式,只有先把通项公式研究明白,然后尽可能转化为我们熟悉的数列问题,由此使问题得到解决.通过对上面(2)(3)(4)问题的解决,你认为研究陌生数列的通项问题有哪些常用方法,要求介绍两个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,二面角
的中点,二面角![]() 等于60°,求直线
等于60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为非零实数,其前
的各项均为非零实数,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意正整数
对任意正整数![]() 恒成立,若存在,求实数
恒成立,若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 做
做![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
①求证:![]() ;
;
②记四边形![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,若
,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() .
.
(1)证明:直线![]() 过定点;
过定点;
(2)若以![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,且切点为线段
相切,且切点为线段![]() 的中点,求该圆的面积.
的中点,求该圆的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com