
分析 (Ⅰ)若函数f(x)是定义在R上的偶函数,则f(x)=f(-x)恒成立,进而可得a值;
(Ⅱ)若a=0,f(x)=log4(4x+1),设x1<x2,判断f(x1)-f(x2)的符号,进而根据函数奇偶的定义,可得函数f(x)在R上是增函数;
(Ⅲ)若不等式f(x)+f(-x)≥mt+m对任意x∈R,t∈[-2,1]恒成立,mt+m≤1对任意t∈[-2,1]恒成立,进而可得实数m的取值范围.
解答 解:(Ⅰ)由函数f(x)是定义在R上的偶函数,则f(x)=f(-x)恒成立,
即${log_4}({4^x}+1)+ax={log_4}({4^{-x}}+1)-ax$,所以$2ax={log_4}\frac{{{4^{-x}}+1}}{{{4^x}+1}}={log_4}\frac{1}{4^x}=-x$,
所以(2a+1)x=0恒成立,则2a+1=0,故$a=-\frac{1}{2}$.(4分)
(Ⅱ)证明:设x1<x2,
那么$f({x_1})-f({x_2})={log_4}({4^{x_1}}+1)-{log_4}({4^{x_2}}+1)={log_4}({\frac{{{4^{x_1}}+1}}{{{4^{x_2}}+1}}})$
因为x1<x2,
所以0<${4}^{{x}_{1}}$<${4}^{{x}_{2}}$,$\frac{{4}^{{x}_{1}}+1}{{4}^{{x}_{2}}+1}∈(0,1)$,$lo{g}_{4}(\frac{{4}^{{x}_{1}}+1}{{4}^{{x}_{2}}+1})$<0,
所以f(x1)-f(x2)<0,
故函数f(x)在定义域R上是单调增函数.(9分)
(Ⅲ)$f(x)+f(-x)={log_4}({4^x}+1)+ax+{log_4}({4^{-x}}+1)-ax={log_4}({4^x}+1)+{log_4}({4^{-x}}+1)$=${log_4}({4^x}+1)({4^{-x}}+1)={log_4}(2+{4^x}+{4^{-x}})$
设$g(r)=2+r+\frac{1}{r}$,其中r=4x,x∈R,r>0,
由双钩函数的图象知,r=1时,g(r)有最小值4.
∴f(x)+f(-x)≥log44=1
所以mt+m≤1对任意t∈[-2,1]恒成立,令h(t)=mt+m,
由$\left\{\begin{array}{l}h(-2)=-2m+m≤1\\ h(1)=m+m≤1\end{array}\right.$解得$-1≤m≤\frac{1}{2}$,(14分)
点评 本题考查的知识点是函数的奇偶性,函数的单调性,恒成立问题,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,$\frac{7}{3}$] | B. | [$\frac{7}{3}$,3] | C. | [2,3] | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
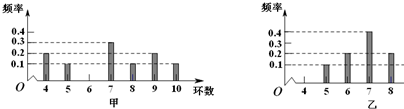
| A. | y1=y2,s1>s2 | B. | y1=y2,s1<s2 | C. | y1>y2,s1=s2 | D. | y1<y2,s1=s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com