Question

3．对于函数f（x）和g（x），设m∈{x∈R|f（x）=0}，n∈{x∈R|g（x）=0}，若存在m、n，使得|m-n|≤1，则称f（x）与g（x）互为“零点关联函数”．若函数f（x）=log₂（x+1）-e^1-x与g（x）=x²-ax-a+3互为“零点关联函数”，则实数a的取值范围为（　　）

• A． [2，$\frac{7}{3}$]
• B． [$\frac{7}{3}$，3]
• C． [2，3]
• D． [2，4]

Answer 1

分析 先得出函数f（x）=e^x-1+x-2的零点为x=1．再设g（x）=x²-ax-a+3的零点为β，根据函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，及新定义的零点关联函数，有|1-β|≤1，从而得出g（x）=x²-ax-a+3的零点所在的范围，最后利用数形结合法求解即可．

解答 解：函数f（x）=log₂（x+1）-e^1-x的零点为x=1．
设g（x）=x²-ax-a+3的零点为β，
若函数f（x）=log₂（x+1）-e^1-x与g（x）=x²-ax-a+3互为“零点关联函数”，
根据零点关联函数，则|1-β|≤1，
∴0≤β≤2，如图．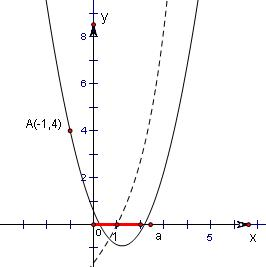

由于g（x）=x²-ax-a+3必过点A（-1，4），
由于g（x）=x²-ax-a+3必过点A（-1，4），
故要使其零点在区间[0，2]上，则
g（0）×g（2）≤0或$\left\{\begin{array}{l}g（0）＞0\\ g（2）＞0\\△≥0\\ 0≤\frac{a}{2}≤2\end{array}\right.$，
解得：2≤a≤3，
实数a的取值范围为[2，3]，
故选：C

点评 先得出函数f（x）=e^x-1+x-2的零点为x=1．再设g（x）=x²-ax-a+3的零点为β，根据函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，及新定义的零点关联函数，有|1-β|≤1，从而得出g（x）=x²-ax-a+3的零点所在的范围，最后利用数形结合法求解即可．