
已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设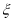 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求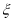 的分布列和数学期望
的分布列和数学期望
(1)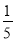 ;(2)
;(2)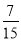 ;(3)分布列(略),
;(3)分布列(略),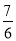 .
.
【解析】
试题分析:(1)4个球均为黑球,即从甲、乙中取出的2个球均为黑球,由于甲、乙相互独立,因此概率为甲中取出黑球的概率与乙中取出黑球概率的乘积;(2)取出4球中恰有1个红球,分两类计算:一类红球来至于甲,二类红球来至于乙;(3)红球个数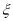 可能取值为0,1,2,3,注意分别对应概率的计算.
可能取值为0,1,2,3,注意分别对应概率的计算.
试题解析:
(1)设“从甲盒内取出的2个球均为黑球”为事件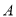 ,
,
“从乙盒内取出的2个球均为黑球”为事件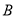 .
.
由于事件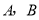 相互独立,且
相互独立,且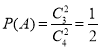 ,
,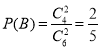 . 2分
. 2分
故取出的4个球均为黑球的概率为 . 4分
. 4分
(2) 设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件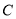 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件 .则
.则
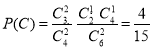 ,
,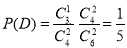 . 6分
. 6分
由于事件 互斥,故取出的4个球中恰有1个红球的概率为
互斥,故取出的4个球中恰有1个红球的概率为
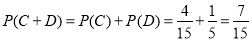 . 8分
. 8分
(3)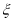 可能的取值为
可能的取值为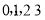 .
.
由(1),(2)得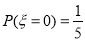 ,
,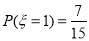 ,
, 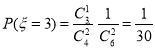 .
.
从而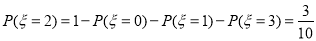 .
.
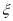 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
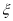 的数学期望
的数学期望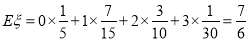 . 12分
. 12分
考点:组合与概率综合应用.


科目:高中数学 来源:2015届重庆一中高二下学期期中考试理科数学试卷(解析版) 题型:解答题
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).

(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为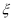 ,求
,求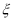 的分布列及数学期望
的分布列及数学期望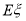 .
.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知圆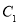 的参数方程为
的参数方程为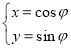 (
(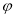 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆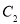 的极坐标方程为
的极坐标方程为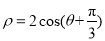 .
.
(1)将圆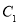 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆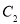 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆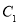 ,
,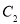 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
将三颗骰子各掷一次,设事件A为“三个点数都不相同”,事件B为“至少出现一个6点”,则概率P(A|B)的值为
A.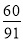 B.
B.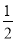 C.
C.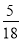 D.
D.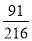
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数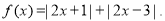
(1)求不等式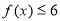 的解集;
的解集;
(2)若关于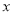 的不等式
的不等式 的解集非空,求实数
的解集非空,求实数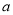 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:填空题
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这项任务,不同的选法有________.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省抚顺市六校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
有6个座位连成一排,现有3人入座,则恰有两个空位相邻的不同坐法是( )种
A.36 B.48 C.72 D.96
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为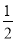 ,乙每次击中目标的概率
,乙每次击中目标的概率 .
.
(1)记甲击中目标的次数为ξ,求ξ的概率分布列及数学期望Eξ;
(2)求甲恰好比乙多击中目标2次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com