练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，a：b：c=3：3：5，
    2sinA-sinB
    sinC
    的值
     
    ．
    考点：正弦定理
    专题：解三角形
    分析：先利用a，b，c的关系式设出分别设出a，b和c，利用正弦定理把题设转换成边，代入即可．
    解答： 解：∵a：b：c=3：3：5，
    ∴设a=3t，b=3t，c=5t，
    由正弦定理知
    2sinA-sinB
    sinC
    =
    2a-b
    c
    =
    6t-3t
    5t
    =
    3
    5
    ，
    故答案为：
    3
    5
    点评：本题主要考查了正弦定理的应用．正弦定理在解三角形问题中常用来对边角问题进行转换．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知向量
    a
    ，
    b
    是两非零向量，在下列四个条件中，能使
    a
    ，
    b
    共线的条件是
     

    A．2
    a
    -3
    b
    =4
    e
    ，
    a
    +2
    b
    =-3
    e

    B．存在相异实数λ，μ，使λ
    a
    +μ
    b
    =0
    C．x
    a
    +y
    b
    =
    0
    （其中实数x，y满足x+y=0）
    D．已知梯形ABCD中，
    AB
    =
    a
    ，
    CD
    =
    b
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若D为△ABC的边BC的中点，△ABC所在平面内有一点P，满足
    PA
    +2
    BP
    +2
    CP
    =0，设
    |
    AP
    |
    |
    PD
    |
    =λ，则λ的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数f（x）=x3-2f′（1）x在x=2处的切线方程
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=
    		log3x-2
    的定义域是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若复数z满足iz=2+4i，则在复平面内，z的共轭复数
    .
    z
    对应的点的坐标是（　　）
    A、（2，4）
    B、（2，-4）
    C、（4，-2）
    D、（4，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线y2-
    x2
    m
    =1的中心在原点O，双曲线两条渐近线与抛物线y2=mx交于A，B两点，且S△OAB=9
    		3
    ，则双曲线的离心率为（　　）
    A、
    		3
    B、2
    C、
    		5
    D、
    		7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    小乐与小波在学了变量的相关性之后，两人约定回家去利用自己各自记录的6-10岁的身高记录作为实验数据，进行回归分析，探讨年龄x（岁）与身高y（cm）之间的线性相关性．经计算小乐与小波求得的线性回归直线分别为l1，l2，在认真比较后，两人发现他们这五年身高的平均值都为110cm，而且小乐的五组实验数据均满足所求的直线方程，小波则只有两组实验数据满足所求直线方程．下列说法错误的是（　　）
    A、直线l1，l2一定有公共点（8，110）
    B、在两人的回归分析中，小乐求得的线性相关系数r=1，小波求得的线性相关系数r∈（0，1）
    C、在小乐的回归分析中，他认为x与y之间完全线性相关，所以自己的身高y（cm）与年龄x（岁）成一次函数关系，利用l1可以准确预测自己20岁的身高
    D、在小波的回归分析中，他认为x与y之间不完全线性相关，所以自己的身高y（cm）与年龄x（岁）成相关关系，利用l2只可以估计预测自己20岁的身高

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如果执行如图的程序框图，那么输出的S=
    2013
    2014
    ，那么判断框内是（　　）
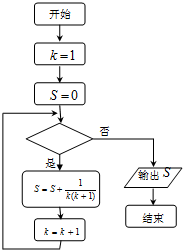
    A、k≤2013？
    B、k≤2014？
    C、k≥2013？
    D、k≥2014？

    查看答案和解析>>

    同步练习册答案