
分析 (1)由一元二次方程的判别式大于等于0得到方程x2+2ax+b2=0有实数根的充要条件为a≥b,用列举法求出a,b是从[0,3]任取的两个整数即从0,1,2,3四个数中任取的两个数,查出满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;
(2)由题意求出点(a,b)所构成的正方形的面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率
解答 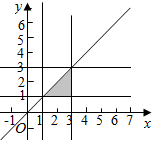 解:(1)在区间[1,3]上任取两整数a、b,共有3×3=9种取法,基本事件共9个,(1,1),(1,2),(1,3),
解:(1)在区间[1,3]上任取两整数a、b,共有3×3=9种取法,基本事件共9个,(1,1),(1,2),(1,3),
(2,1),(2,2),(2,3),(3,1),(3,2),(3,3).其中第一个数表示a的取值,第二个数表示b的取值
使二次方程x2+2ax+b2=0有实数根的事件为A,A中A,B满足a≥b,则事件A中包含6基本事件.
事件A发生的概率为P(A)=$\frac{6}{9}=\frac{2}{3}$;
(2)试验的全部结果所构成的区域为{(a,b)|1≤a≤3,1≤b≤3}.
构成事件A的区域为{(a,b)|1≤a≤3,1≤b≤3,a≥b}.
如图,
∴所求的概率P(A)=$\frac{\frac{1}{2}×2×2}{2×2}=\frac{1}{2}$.
点评 本题考查了古典概型以及几何概型的概率计算公式,关键是理解(2)的测度比,是基础题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 4π | C. | 6π | D. | 5π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\left.x\right|2kπ-\frac{3}{4}π<x<2kπ+\frac{π}{4},k∈Z}\right\}$ | B. | $\left\{{\left.x\right|2kπ+\frac{π}{4}<x<2kπ+\frac{5}{4}π,k∈Z}\right\}$ | ||
| C. | $\left\{{\left.x\right|kπ-\frac{π}{4}<x<kπ+\frac{π}{4},k∈Z}\right\}$ | D. | $\left\{{\left.x\right|kπ+\frac{π}{4}<x<kπ+\frac{3}{4}π,k∈Z}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪[2,+∞) | B. | (-1,2) | C. | (-∞,-1]∪[-$\frac{1}{2}$,+∞) | D. | (-1,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线y2=2px(p>0),过点Q(4,0)作动直线l交抛物线于A,B两点,且OA⊥OB(O为坐标原点).
已知抛物线y2=2px(p>0),过点Q(4,0)作动直线l交抛物线于A,B两点,且OA⊥OB(O为坐标原点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com