Question

【题目】如图所示，已知圆O1与圆O2相交于A，B两点，过点A作圆O1的切线交圆O2于点C，过点B作两圆的割线，分别交圆O1 ， 圆O2于点D，E，DE与AC相交于点P．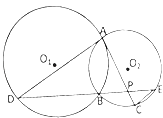

（1）求证：AD∥EC；
（2）若AD是圆O2的切线，且PA=3，PC=1，AD=6，求DB的长．

Answer 1

【答案】
（1）证明：连接AB，

∵AC是圆O1的切线，∴∠BAC=∠D，

又∵∠BAC=∠E，∴∠D=∠E，∴AD∥EC

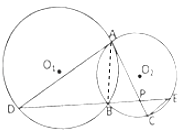
（2）解：设PB=x，PE=y，

∵PA=3，PC=1，∴xy=3①，

∵AD∥EC，∴ ，且DP=3y

由AD是圆O2的切线，∴AD2=DBDE，∴62=（3y﹣x）4y②

由①②可得， ，∴BD=3y﹣x=

【解析】（1）连接AB，根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D，又根据同弧所对的圆周角相等得到∠BAC=∠E，等量代换得到∠D=∠E，根据内错角相等得到两直线平行即可；（2）根据切割线定理得到AD2=DBDE，利用AD是圆O2的切线，AD2=DBDE，由此即可求DB的长．