Question

1．已知定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=（x-a）²-a²，且对x∈R，恒有f（x+1）≥f（x），则实数a的取值范围为（-∞，$\frac{1}{4}$]．

Answer 1

分析 根据函数奇偶性的性质求出函数f（x）的解析式，讨论a的取值，作出函数f（x）的图象，利用图象平移以及数形结合进行求解即可．

解答 解：∵定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=（x-a）²-a²，
∴若x＜0，则-x＞0，
则f（-x）=（-x-a）²-a²=-f（x），
即f（x）=-（x+a）²+a²，x＜0，
若a≤0，则f（x）=$\left\{\begin{array}{l}{（x-a）^{2}-{a}^{2}}&{x≥0}\\{-（x+a）^{2}+{a}^{2}}&{x＜0}\end{array}\right.$在定义域上为增函数，恒有f（x+1）≥f（x）成立，
当a＞0时，函数f（x）的图象如图：
∵f（x+1）的图象可以函数是由函数f（x）的图象向左平移1个单位得到的，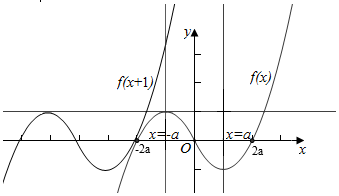
需要函数f（x）的图象至少向左平移2a-（-2a）=4a个单位才能满足f（x+1）≥f（x）恒成立，
则4a≤1，即0＜a≤$\frac{1}{4}$，
综上a≤$\frac{1}{4}$，
故答案为：（-∞，$\frac{1}{4}$]

点评 本题主要考查不等式恒成立问题，利用函数奇偶性求出函数的解析式，以及利用分类讨论和数形结合以及图象平移关系是解决本题的关键．综合性较强，难度较大．