练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

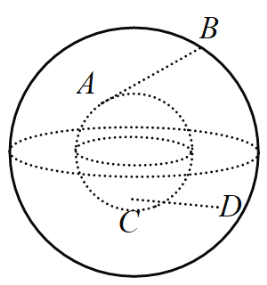
    【题目】如图两个同心球，球心均为点，其中大球与小球的表面积之比为3:1，线段与是夹在两个球体之间的内弦，其中两点在小球上，两点在大球上，两内弦均不穿过小球内部.当四面体的体积达到最大值时，此时异面直线与的夹角为，则（ ）

    A.B.C.D.

    【答案】A

    【解析】

    首先判断出正方体内切球和外接球的半径比为，内切球和外接球的表面积之比为，符合题意中的小球和大球的比例.判断当四面体体积最大时，的位置关系，作出异面直线所成的角，解直角三角形求得.

    设正方体的边长为，则其内切球半径为，外接球的半径为，所以内切球和外接球的表面积之比为，符合题意中的小球和大球的比例. 依题意最长为，最长为小球的直径.由于三角形的面积，若为定值，则时面积取得最大值.画出图像如下图所示，其中分别是所在正方形的中心，是正方体内切球与外接球的球心..由于，故此时四面体的体积最大.

    由于，所以四边形为平行四边形，所以，所以是异面直线和所成的角.所以由于，设是的中点，则，所以，所以.

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是( )

    A.两条相交直线在同一平面内的射影必为相交直线

    B.不共线三点到平面的距离相等，则这三点确定的平面不一定与平面平行

    C.对确定的两异面直线，过空间任一点有且只有一个平面与两异面直线都平行

    D.两个相交平面的交线是一条线段

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的点．

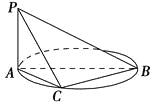
    (1)求证：平面PAC⊥平面PBC；

    (2)若AB＝2，AC＝1，PA＝1，求二面角C－PB－A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大提出，加快水污染防治，建设美丽中国.根据环保部门对某河流的每年污水排放量（单位：吨）的历史统计数据，得到如下频率分布表：

    将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立.

    （1）求在未来3年里，至多1年污水排放量的概率；（2）该河流的污水排放对沿河的经济影响如下：当时，没有影响；当时，经济损失为10万元；当时，经济损失为60万元.为减少损失，现有三种应对方案：

    方案一：防治350吨的污水排放，每年需要防治费3.8万元；

    方案二：防治310吨的污水排放，每年需要防治费2万元；

    方案三：不采取措施.

    试比较上述三种文案，哪种方案好，并请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取，他们分别被哪个学校录取，同学们做了如下的猜想

    甲同学猜：曾玉被武汉大学录取，李梦被复旦大学录取

    同学乙猜：刘云被清华大学录取，张熙被北京大学录取

    同学丙猜：曾玉被复旦大学录取，李梦被清华大学录取

    同学丁猜：刘云被清华大学录取，张熙被武汉大学录取

    结果，恰好有三位同学的猜想各对了一半，还有一位同学的猜想都不对

    那么曾玉、刘云、李梦、张熙四人被录取的大小可能是（ ）

    A.北京大学、清华大学、复旦大学、武汉大学

    B.武汉大学、清华大学、复旦大学、北京大学

    C.清华大学、北京大学、武汉大学 、复旦大学

    D.武汉大学、复旦大学、清华大学、北京大学

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若、是两个相交平面，则在下列命题中，真命题的序号为（ ）

    ①若直线，则在平面内一定不存在与直线平行的直线．

    ②若直线，则在平面内一定存在无数条直线与直线垂直．

    ③若直线，则在平面内不一定存在与直线垂直的直线．

    ④若直线，则在平面内一定存在与直线垂直的直线．

    A. ①③ B. ②③ C. ②④ D. ①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    ①命题“若，则方程无实根”的否命题；

    ②命题“在中，，那么为等边三角形”的逆命题；

    ③命题“若，则”的逆否命题；

    ④“若，则的解集为”的逆命题；

    其中真命题的序号为（ ）

    A.①②③④B.①②④C.②④D.①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了适应高考改革，某中学推行“创新课堂”教学．高一平行甲班采用“传统教学”的教学方式授课，高一平行乙班采用“创新课堂”的教学方式授课，为了比较教学效果，期中考试后，分别从两个班中各随机抽取名学生的成绩进行统计分析，结果如下表：（记成绩不低于分者为“成绩优秀”）

    分数

    甲班频数

    乙班频数

    （Ⅰ）由以上统计数据填写下面的列联表，并判断是否有以上的把握认为“成绩优秀与教学方式有关”？

    甲班

    乙班

    总计

    成绩优秀

    成绩不优秀

    总计

    （Ⅱ）现从上述样本“成绩不优秀”的学生中，抽取人进行考核，记“成绩不优秀”的乙班人数为，求的分布列和期望．

    参考公式：，其中．

    临界值表

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘.如下图所示，从左到右有ABC三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则:一次只能移动一个盘子且大盘子不能在小盘子上面，则移动的次数为_______(用表示)

    ABC

    查看答案和解析>>

    同步练习册答案