
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
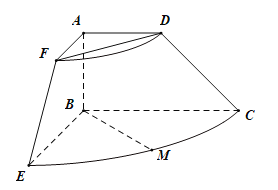
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中;
中;
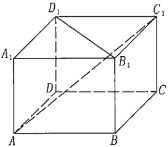
已知三个论断:(1)四棱柱![]() 是直四棱柱;(2)底面
是直四棱柱;(2)底面![]() 是菱形;(3)
是菱形;(3)![]() .
.
以其中两个论断作条件,余下一个为结论,可以得到三个命题,其中有几个是真命题?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)若![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
(2)若![]() 过点
过点![]() ,射线
,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时直线
能否为平行四边形?若能,求此时直线![]() 斜率;若不能,说明理由.
斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为2016年至2019年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 | 1 | 2 | 3 | 4 |
线下销售额 | 95 | 165 | 230 | 310 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该百货零售企业的线下销售额;
的线性回归方程,并预测2020年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
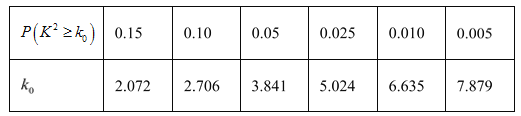
参考公式及数据:
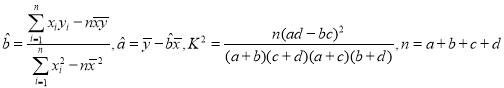 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①“![]() ”是“
”是“![]() ”的充分不必要条件;②命题“
”的充分不必要条件;②命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件
”;③小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() 为“4个人去的景点不相同”,事件
为“4个人去的景点不相同”,事件![]() 为“小赵独自去一个景点”,则
为“小赵独自去一个景点”,则![]() ;④设
;④设![]() ,其正态分布密度曲线如图所示,那么向正方形
,其正态分布密度曲线如图所示,那么向正方形![]() 中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若
中随机投掷10000个点,则落入阴影部分的点的个数的估计值是6587.(注:若![]() ,则
,则![]() ,
,![]() )其中正确说法的个数为( )
)其中正确说法的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
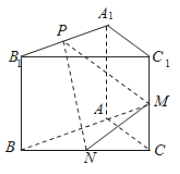
【题目】如图,已知三棱柱![]() 中,侧棱与底面垂直,且
中,侧棱与底面垂直,且![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求证:不论![]() 取何值,总有
取何值,总有![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角A,B,C所对的边分别是a,b,c,其面积S
的内角A,B,C所对的边分别是a,b,c,其面积S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com