
【题目】已知![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)若![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
(2)若![]() 过点
过点![]() ,射线
,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时直线
能否为平行四边形?若能,求此时直线![]() 斜率;若不能,说明理由.
斜率;若不能,说明理由.
科目:高中数学 来源: 题型:
【题目】某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
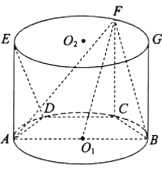
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表:
送餐距离(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.

其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图

以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为
,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为![]() 的中点.
的中点.
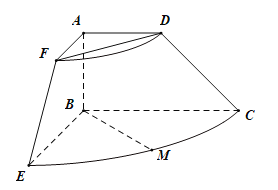
(1)求证:![]() ;
;
(2)求异面直线BM与EF所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com