
【题目】某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
【答案】投资人用4万元投资甲项目,6万元投资乙项目,取得的盈利最大为7万元
【解析】
本试题主要是考查了线性规划的运用。
根据已知条件设投资人分别用x万元、y万元投资甲、乙两个项目,由题意:
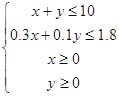 ,并且得到目标函数
,并且得到目标函数![]() ,
,
然后运用平移法得到最值。
解:设投资人分别用x万元、y万元投资甲、乙两个项目,由题意:
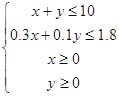 ,目标函数
,目标函数![]() ,
,
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域。
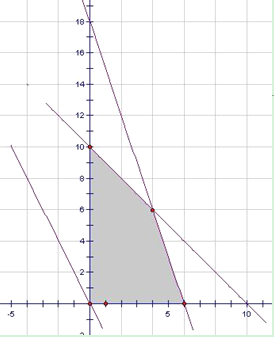
作直线![]() ,并作平行于直线
,并作平行于直线![]() 的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线
的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线![]() 的距离最大,其中M点是直线
的距离最大,其中M点是直线![]() 和直线
和直线![]() 的交点,解方程组
的交点,解方程组![]() 得
得![]() ,此时
,此时![]() (万元),
(万元),![]() ,当
,当![]() 时,
时,![]() 取得最大值。
取得最大值。
答:投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8 万元的前提下,使可能的盈利最大。


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
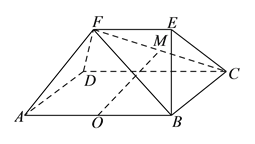
【题目】如图所示,已知多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
(![]() )求证:
)求证: ![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若过
)若过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题 ②“正多边形都相似”的逆命题
③“若m>0,则x2+x-m=0有实根”的逆否命题④“若x-![]() 是有理数,则x是
是有理数,则x是
无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论不正确的是________(填序号).
①各个面都是三角形的几何体是三棱锥;
②以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥;
③棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥;
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.

(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)将频率分布直方图中的五组从左到右依次命名为第一组,第二组,…,第五组.从第一组和第五组中的所有天数中抽出两天,记它们的空气质量指数分别为![]() ,
, ![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]()
![]() 的切线,
的切线, ![]() 为坐标原点,切点为
为坐标原点,切点为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 是圆
是圆![]() 上位于第一象限内的任意一点,过点
上位于第一象限内的任意一点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,且
,且![]() 交
交![]() 轴于点
轴于点![]() ,交y轴于点
,交y轴于点![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极值;
的极值;
(3)若函数![]() 在区间
在区间![]() 上是增函数,试确定
上是增函数,试确定![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 不存在极值.当
不存在极值.当![]() 时,
时,
![]() 有极小值
有极小值![]() 无极大值.(3)
无极大值.(3)![]() .
.
【解析】试题分析:
(1)当![]() 时,求得
时,求得![]() ,得到
,得到![]() 的值,即可求解切线方程.
的值,即可求解切线方程.
(2)由定义域为![]() ,求得
,求得![]() ,分
,分![]() 和
和![]() 时分类讨论得出函数的单调区间,即可求解函数的极值.
时分类讨论得出函数的单调区间,即可求解函数的极值.
(3)根据题意![]() 在
在![]() 上递增,得
上递增,得![]() 对
对![]() 恒成立,进而求解实数
恒成立,进而求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,∴切线方程为
,∴切线方程为![]() .
.
(2)定义域为![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 不存在极值.
不存在极值.
当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 有极小值
有极小值![]() 无极大值.
无极大值.
(3)∵![]() 在
在![]() 上递增,∴
上递增,∴![]() 对
对![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() .
.
点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)考查数形结合思想的应用.
【题型】解答题
【结束】
22
【题目】已知圆![]() :
: ![]() 和点
和点![]() ,
, ![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和
的垂直平分线和![]() 相交于点
相交于点![]() ,
, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,直线
轴正半轴的交点,直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() ,
, ![]() 的斜率分别是
的斜率分别是![]() ,
, ![]() ,若
,若![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com