
【题目】已知函数![]() .
.
(1)试讨论![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)求导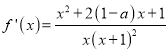 ,
, ![]() ,讨论
,讨论![]() 两种情况即可得解(2)
两种情况即可得解(2)![]() ,
, ![]() 由题意
由题意![]() ,
, ![]() 是方程
是方程![]() 的两个根,所以
的两个根,所以![]() ,①
,① ![]() ,②联立①②得出
,②联立①②得出![]() ,所以
,所以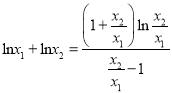 令
令![]() ,所以
,所以![]() ,
, ![]() ,因此只需证明当
,因此只需证明当![]() 时,不等式
时,不等式![]()
![]() 成立即可,即不等式
成立即可,即不等式![]() 成立,构造差函数研究单调性即可得证.
成立,构造差函数研究单调性即可得证.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, 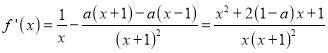 ,
,
令![]() ,
, ![]() ,
,
当![]() 时,解得
时,解得![]() ,此时
,此时![]() 在
在![]() 上恒成立,
上恒成立,
故可得![]() 在
在![]() 上恒成立,即当
上恒成立,即当![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,解得
时,解得![]() 或
或![]() ,
,
方程![]() 的两根为
的两根为![]() 和
和![]() ,
,
当![]() 时,可知
时,可知![]() ,
, ![]() ,此时在
,此时在![]() 上
上![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,易知
时,易知![]() ,
, ![]() ,此时可得
,此时可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上可知,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在区间
在区间![]() 和区间
和区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(2)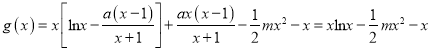 ,
,
![]() ,由题意
,由题意![]() ,
, ![]() 是方程
是方程![]() 的两个根,所以
的两个根,所以![]() ,①
,①
![]() ,②
,②
①②两式相加可得![]() ,③
,③
①②两式相减可得![]() ,④
,④
由③④两式消去![]() 可得
可得![]() ,
,
所以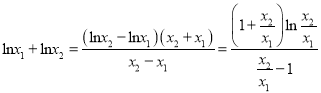 ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
, ![]() ,
,
因此只需证明当![]() 时,不等式
时,不等式![]()
![]() 成立即可,即不等式
成立即可,即不等式![]() 成立.
成立.
设函数![]() ,由(1)可知,
,由(1)可知, ![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,即证得当
,即证得当![]() 时,
时, ![]() ,亦即证得
,亦即证得![]() ,
,
所以![]() ,即证得
,即证得![]() .
.


科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn.已知2Sn=3n+3.
(1)求{an}的通项公式;
(2)若数列{bn}满足anbn=log3an,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l的参数方程为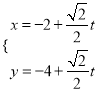 ,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是
(m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)设![]() (其中
(其中![]() 为f (x)的导函数),证明:对任意x > 0,都有
为f (x)的导函数),证明:对任意x > 0,都有![]() .
.
(注: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() =
=![]() x+
x+![]() 必过(
必过(![]() ,
,![]() );
);
④在一个2×2列联表中,由计算得K2=13.079,则有99%以上的把握认为这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
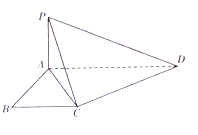
(Ⅰ)![]() 上是否存在点
上是否存在点![]() 使
使![]() 平面
平面![]() ,若存在,指出
,若存在,指出![]() 的位置并证明,若不存在,请说明理由;(Ⅱ)证明:
的位置并证明,若不存在,请说明理由;(Ⅱ)证明: ![]() ;
;
(Ⅲ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com