
| 60分以下 | 61-t0分 | t1-80分 | 81-90分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 1q |
| 乙班(人数) | 4 | 8 | 13 | 1e | 10 |
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(2,4) | B.(1.5,2) | C.(1,2) | D.(1.5,4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
| |||||||
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①③ | B.②④ | C.①④ | D.都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

 ;
; ;
;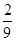 ;
; ;
; .
.| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的. ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com