
分析 利用导数法求出f(x)=ax-sinx为R上的增函数等价命题,进而根据充要条件的定义,可判断①;
求出函数$f(x)=-\frac{1}{3}{x^3}+x+1$的零点个数,可判断②;
求出从A,B中各任意取一个数,则这两数之和等于4的概率,可判断③;
求出圆心C的轨迹方程,可判断④;
求出使不等式ex≥x+a恒成立,的实数a的取值范围,可判断⑤.
解答 解:当f(x)=ax-sinx时,f′(x)=a-cosx,当a≥1时,f′(x)≥0在R上恒成立,f(x)=ax-sinx为R上的增函数,
由{a|a>2}?{a|a≥1},故“a>2”是“f(x)=ax-sinx为R上的增函数”的充分不必要条件,即①正确;
当函数$f(x)=-\frac{1}{3}{x^3}+x+1$时,f′(x)=-x2+1,令f′(x)=0,则x=±1,根据三次函数的图象和性质,可得当x=-1时,f(x)的极小值$\frac{1}{3}$>0,故f(x)仅有一个零点,故②错误;
集合A={2,3},B={1,2,3},从A,B中各任意取一个数共有2×3=6种情况,其中这两数之和等于4有(2,2),(3,1)两种情况,故这两数之和等于4的概率是$\frac{2}{6}$=$\frac{1}{3}$,故③正确;
动圆C既与定圆(x-2)2+y2=4相外切,又与y轴相切,则圆心C的轨迹方程是y2=8x(x≠0)或y=0(x<0),故④错误;
若对任意的正数x,不等式ex≥x+a恒成立,即a≤ex-x对任意的正数x恒成立,令h(x)=ex-x,则h′(x)=ex-1,当x>0时,h′(x)>0恒成立,故h(x)在(0,+∞)上为增函数,
则a≤h(0)=1,故⑤正确;
故正确的命题序号是①③⑤;
故答案为:①③⑤
点评 本题以命题的真假判断为载体,考查了充要条件,函数的单调性,函数的零点,概率,直线与圆的位置关系,圆与圆的位置关系,轨迹方程,恒成立问题等知识点,综合性强,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{-\sqrt{2},1}]$ | C. | $[{-1,\sqrt{2}}]$ | D. | $[{-\sqrt{2},\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
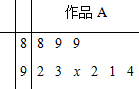 我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
我校开展“爱我河南,爱我方城”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示,记分员在去掉一个最高分和一个最低分后,计算的平均分为91,复核员在复核时,发现一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$(e x-e -x) | B. | $\frac{1}{2}$(e x+e -x) | C. | e x-e -x | D. | e x+e -x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com