练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，三个内角A，B，C的对边分别为a，b，c，其中c＝2，且 ＝＝.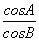

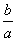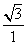    (1)求证：△ABC是直角三角形；

    (2)设圆O过A，B，C三点，点P位于劣弧上，∠PAB＝θ，用θ的三角函数表示△PAC的面积，并求△PAC面积最大值．


     (1)证明：由正弦定理得＝，

    整理为sin Acos A＝sin Bcos B，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，

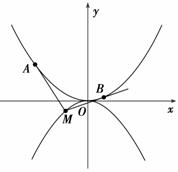
    抛物线C1：x2＝4y，C2：x2＝－2py(p＞0)．点M(x0，y0)在抛物线C2上，过M作C1的切线，切点为A，B(M为原点O时，A，B重合于O)．当x0＝1－时，切线MA的斜率为－.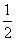

    (1)求p的值；

    (2)当M在C2上运动时，求线段AB中点N的轨迹方程(A，B重合于O时，中点为O)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题p：|2x－3|>1，命题q：log(x2＋x－5)<0，则綈p是綈q的____________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两点A(－1,2)、B(m,3)．

    (1)求直线AB的方程；

    (2)已知实数m∈，求直线AB的倾斜角α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在斜度一定的山坡上一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°，向山顶前进100 m后，又从点B测得斜度为45°，假设建筑物高50 m，设山对于地平面的斜度为θ，则cos θ＝____________.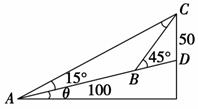

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C所对的边分别为a，b，c，S表示△ABC的面积，若acos B＋bcos A＝csin C，S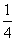＝(b2＋c2－a2)，则B＝(　　)

    A．90°     B．60°      C．45°       D．30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C所对的边分别为a，b，c，且满足csin A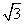＝acos C.

    (1)求角C的大小；

    (2)求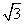sin A－sin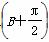的最大值，并求取得最大值时角A，B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝(sin x＋cos x)(sin x－cos x)是(　　)

    A．奇函数且在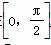上单调递增

    B．奇函数且在上单调递增

    C．偶函数且在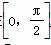上单调递增

    D．偶函数且在上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x2＋(sin α－2cos α)x＋1是偶函数，则sin αcos α＝(　　)

    A.　        B．－          C．±　        D．0

    查看答案和解析>>

    同步练习册答案