
如图,
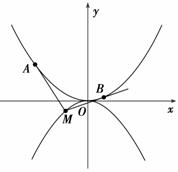
抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1- 时,切线MA的斜率为-
时,切线MA的斜率为-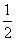 .
.
(1)求p的值;
(2)当M在C 2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
解析:(1)因为抛物线C1:x2=4y上任意一点(x,y )的切线斜率为y′=
)的切线斜率为y′=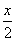 ,且切线MA的斜率为-
,且切线MA的斜率为-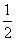 ,所以A点坐标为
,所以A点坐标为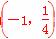 ,故切线MA的方程为y=-
,故切线MA的方程为y=-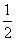 (x+1)+
(x+1)+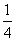 .
.
因为点M(1- ,y0)在切线MA及抛物线C2上,于是
,y0)在切线MA及抛物线C2上,于是
y0=-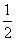 (2-
(2- )+
)+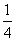 =-
=-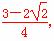 ,①
,①
y0=-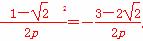 .②
.②
由①②得p=2.
(2)设N( x,y),A
x,y),A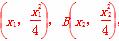 ,x1≠x2,
,x1≠x2,
由N为线段AB中点知
x=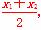 ,③
,③
y=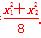 .④
.④
切线MA、MB的方程为
y=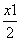 (x-x1)+
(x-x1)+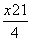 ,⑤
,⑤
y= (x-x2)+
(x-x2)+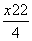 .⑥
.⑥
由⑤⑥得MA,MB的交点M(x0,y0)的坐标为
x0=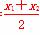
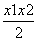 ,y0=
,y0=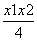 .
.
因为点M(x0,y0)在C2上,即x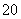 =-4y0,
=-4y0,
所以x1x2=-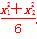 .⑦
.⑦
由③④⑦得x2=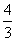 y,x≠0.
y,x≠0.
当x1=x2时,A,B重合于原点O,AB中点N为O,坐标满足x2=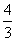 y.
y.
因此AB中点N的轨迹方程为x2=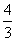 y.
y.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2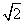 .记动点P的轨迹为W.
.记动点P的轨迹为W.
(1)求W的方程;
(2)若A,B是W上的不同两点,O是坐标原点,求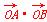 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C的方程为x2+(y-4)2=4,点O是坐标原点.直线l:y=kx与圆C交于M,N两点.
(1)求k的取值范围;
(2)设Q(m,n)是线段MN上的点,且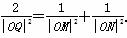 请将n表示为m的函数.
请将n表示为m的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆(x+2)2+y2=36的圆心为M,设A为圆上任一点,N(2,0),线段AN的垂直平分线交MA于点P,则动点P的轨迹是(  )
)
A.圆 B.椭圆 C.双曲线 D.抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点A(-1,0),B(1,0),动点M的轨迹曲线C满足∠AMB=2θ,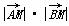 cos2 θ=3.
cos2 θ=3.
(1)求曲线C的方程;
(2)试探究曲线C上是否存在点P,使直线PA与PB的斜率kPA·kPB=1.若存在,请指出共有几个这样的点,并说明理由(不必具体求出这些点的坐标).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:幂函数的图象不过第四象限,命题q:指数函数都是增函数.则下列命题中为真命题的是( )
A.(┓p)∨q B.p∧q
C.(┓p)∨(┓q) D.(┓p)∧(┓q)
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且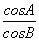 =
=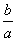 =
=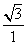 .
.
(1)求证:△ABC是直角三角形;
(2)设圆O过A,B,C三点,点P位于劣弧 上,∠PAB=θ,用θ的三角函数表示△PAC的面积,并求△PAC面积最大值.
上,∠PAB=θ,用θ的三角函数表示△PAC的面积,并求△PAC面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com