
 x,求使f(x)=-
x,求使f(x)=- 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数. x,设-1≤x≤0,则0≤-x≤1,∴f(-x)=
x,设-1≤x≤0,则0≤-x≤1,∴f(-x)= (-x)=-
(-x)=- x.
x. x,即f(x)=
x,即f(x)=  x.
x.  x(-1≤x≤1) 又设1<x<3,则-1<x-2<1,
x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, (x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
(x-2), 又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x), (x-2),∴f(x)=-
(x-2),∴f(x)=- (x-2)(1<x<3).
(x-2)(1<x<3). 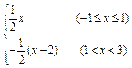 由f(x)=-
由f(x)=- ,解得x=-1.
,解得x=-1. 的所有x="4n-1" (n∈Z).
的所有x="4n-1" (n∈Z). 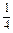 ≤n≤
≤n≤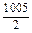 ,又∵n∈Z,∴1≤n≤502 (n∈Z),
,又∵n∈Z,∴1≤n≤502 (n∈Z), .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
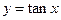 在其定义域内是增函数;②函数
在其定义域内是增函数;②函数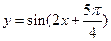 的图象关于直线
的图象关于直线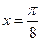 对称;③函数
对称;③函数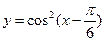 的最小正周期是2π;④函数
的最小正周期是2π;④函数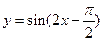 是偶函数.其中正确结论的序号是 .
是偶函数.其中正确结论的序号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com