
分析 (1)令n=n-1再和条件式相减得出递推式,从而得出{an}的奇数项和偶数项均为等比数列进而求出通项公式;
(2)化简bn,利用错位相减法求和.
解答 解:(1)∵an+2=3Sn-Sn+1+3,∴an+1=3Sn-1-Sn+3,
两式相减得:an+2-an+1=3an-an+1,即an+2=3an.
又a1=1,s2=2,∴a1=a2=1.
∴{an}的奇数项和偶数项均组成以1为首项,以3为公比的等比数列,
∴an=$\left\{\begin{array}{l}{{3}^{\frac{n-1}{2},n为奇数}}\\{{3}^{\frac{n-2}{2},n为偶数}}\end{array}\right.$.
(2)由(1)可知a2n+1=3n,a2n=3n-1,
∴bn=$\frac{lo{g}_{3}{a}_{2n+1}}{{a}_{2n}}$=$\frac{n}{{3}^{n-1}}$,
∴Tn=1+$\frac{2}{3}$+$\frac{3}{{3}^{2}}$+$\frac{4}{{3}^{3}}$+…+$\frac{n}{{3}^{n-1}}$,
∴$\frac{{T}_{n}}{3}$=$\frac{1}{3}$+$\frac{2}{{3}^{2}}$+$\frac{3}{{3}^{3}}$+$\frac{4}{{3}^{4}}$+…+$\frac{n}{{3}^{n}}$,
∴$\frac{2{T}_{n}}{3}$=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n-1}}$-$\frac{n}{{3}^{n}}$=$\frac{1-(\frac{1}{3})^{n}}{1-\frac{1}{3}}$-$\frac{n}{{3}^{n}}$=$\frac{3}{2}$(1-$\frac{1}{{3}^{n}}$)-$\frac{n}{{3}^{n}}$,
∴Tn=$\frac{9}{4}$(1-$\frac{1}{{3}^{n}}$)-$\frac{n}{2}$•$\frac{1}{{3}^{n-1}}$.
点评 本题考查了数列通项公式的求法,错位相减法求和,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
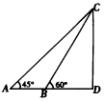 如图所示,A,B,D在地平面同一直线上,AB=20,从A,B两地测得C点的仰角分别为45°和60°,则C点离地面的高CD等于( )
如图所示,A,B,D在地平面同一直线上,AB=20,从A,B两地测得C点的仰角分别为45°和60°,则C点离地面的高CD等于( )| A. | $10(\sqrt{3}-1)$ | B. | $10(\sqrt{3}+1)$ | C. | $10(3-\sqrt{3})$ | D. | $10(3+\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | B. | f(x)=2x-1,g(x)=2x+1 | ||
| C. | f(x)=x2,g(x)=$\root{3}{{x}^{6}}$ | D. | f(x)=1,g(x)=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,5] | B. | [$\frac{3}{2}$,11] | C. | [$\frac{1}{5}$,$\frac{2}{3}$] | D. | [$\frac{1}{5}$,$\frac{3}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com