
| A. | 12π | B. | 32π | C. | 36π | D. | 48π |
分析 由题意推出MN⊥平面SAC,即SB⊥平面SAC,∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球,正方体的对角线就是球的直径,求出直径即可求出球的表面积积.
解答 解:∵M,N分别为棱SC,BC的中点,∴MN∥SB
∵三棱锥S-ABC为正棱锥,
∴SB⊥AC(对棱互相垂直),∴MN⊥AC
又∵MN⊥AM,而AM∩AC=A,
∴MN⊥平面SAC,∴SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°
以SA,SB,SC为从同一定点S出发的正方体三条棱,
将此三棱锥补成以正方体,则它们有相同的外接球,
正方体的对角线就是球的直径.∴2R=$\sqrt{3}$SA=6,∴R=3,
∴S=4πR2=36π.
故选:C
点评 本题考查了三棱锥的外接球的体积,考查空间想象能力.三棱锥扩展为正方体,它的对角线长就是外接球的直径,是解决本题的关键.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.
如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )| A. | 70 | B. | 72 | C. | 74 | D. | 76 |
查看答案和解析>>
科目:高中数学 来源:2017届山西临汾一中高三10月月考数学(理)试卷(解析版) 题型:选择题
已知双曲线 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线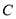 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若 的面积为
的面积为 ,则双曲线
,则双曲线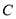 的离心率为( )
的离心率为( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com