Question

4．如图所示三棱锥A-BCD，其中AB=CD=5，AC=BD=6，AD=BC=7，则该三棱锥外接球的表面积为55π．

Answer 1

分析 三棱锥A-BCD的三条侧棱两两相等，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，然后解答即可．

解答 解：如图，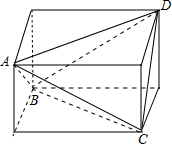
∵三棱锥A-BCD的三条侧棱两两相等，∴把它扩展为长方体，
它也外接于球，且此长方体的面对角线的长分别为：5，6，7，体对角线的长为球的直径，
d=$\sqrt{\frac{1}{2}（{5}^{2}+{6}^{2}+{7}^{2}）}$=$\sqrt{55}$．
∴它的外接球半径是$\frac{\sqrt{55}}{2}$．
外接球的表面积是 4π$•（\frac{\sqrt{55}}{2}）^{2}=55π$．
故答案为：55π．

点评 本题考查球的体积，考查空间想象能力，计算能力，解答的关键是构造球的内接长方体，利用体对角线的长为球的直径解决问题，是中档题．