
分析 连结MF2,作过A、F2的直线交椭圆于M1、M2两点.根据椭圆的定义算出|MF1|+|MA|=10-|MF2|+|MA|=10+(|MA|-|MF2|),由平面几何知识得-|AF2|≤|MA|-|MF2|≤|AF2|,再利用两点间的距离公式加以计算,可得|MF1|+|MA|的最值.
解答 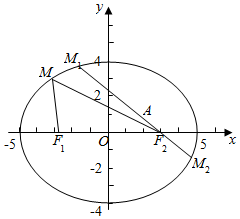 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的a=5,b=4,c=$\sqrt{{a}^{2}-{b}^{2}}$=3,
解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的a=5,b=4,c=$\sqrt{{a}^{2}-{b}^{2}}$=3,
由椭圆的定义可得,|MF1|+|MF2|=2a=10,
即|MF1|=10-|MF2|,
则|MF1|+|MA|=10-|MF2|+|MA|=10+(|MA|-|MF2|),
当点M位于M1时,|MA|-|MF2|的差最小,
其值为-|AF2|=-$\sqrt{(3-2)^{2}+(0-1)^{2}}$=-$\sqrt{2}$,
此时|MF1|+|MA|也得到最小值,其值为10-$\sqrt{2}$;
当点M位于M2时,|MA|-|MF2|的差最大,其值为|AF2|=$\sqrt{2}$,
此时|MF1|+|MA|也得到最大值,其值为10+$\sqrt{2}$.
点评 本题给出椭圆的右焦点,椭圆内一个定点,求椭圆上动点M到定点、焦点两点的距离和的最值.着重考查了两点间的距离公式、椭圆的定义与标准方程等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
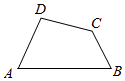 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°,则四边形ABCD的面积的最大值是3$\sqrt{3}$.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°,则四边形ABCD的面积的最大值是3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com