
分析 (1)根据条件运用离心率公式和菱形的面积公式,求出a,b,即可求椭圆C的标准方程;
(2)①设PQ的方程为:x=my+1代入椭圆方程,利用根与系数之间的关系求出OG和ON的斜率,即可得证;
②讨论,当m=0时,求出N的坐标,|NF|,|PQ|的长,计算可得$\frac{|PQ|}{|FN|}$=1;当m≠0时,求得|NF|,运用弦长公式可得|PQ|,再由换元法,设t=m2+1,转化为t的函数,判断单调性,可得所求范围.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{1}{2}$•2a•2b=4$\sqrt{3}$,
又a2-b2=c2,
解得a=2,c=1,b=$\sqrt{3}$,
故所求椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)①证明:设直线PQ的方程为:x=my+1,代入椭圆方程3x2+4y2=12,
得(3m2+4)y2+6my-9=0,
则判别式△=36m2+4×9(3m2+4)>0,
设P(x1,y1),Q(x2,y2),PQ的中点G(x0,y0),
则y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
则y0=$\frac{1}{2}$(y1+y2)=-$\frac{3m}{3{m}^{2}+4}$,x0=my0+1=$\frac{4}{3{m}^{2}+4}$,
即G($\frac{4}{3{m}^{2}+4}$,-$\frac{3m}{3{m}^{2}+4}$),
kOG=-$\frac{3m}{3{m}^{2}+4}$•$\frac{3{m}^{2}+4}{4}$=-$\frac{3m}{4}$,
设直线FN的方程为:y=-m(x-1),得N点坐标为(4,-3m),
∵kON=-$\frac{3m}{4}$,
∴kOG=kON,
即线段PQ的中点在直线ON上;
②当m=0时,PQ的中点为F,N(4,0),
则|NF|=3,|PQ|=$\frac{2{b}^{2}}{a}$=3,$\frac{|PQ|}{|FN|}$=1;
当m≠0时,|NF|=$\sqrt{(4-1)^{2}+(-3m)^{2}}$=3$\sqrt{{m}^{2}+1}$,
|PQ|=$\sqrt{1+\frac{1}{{{k}_{PQ}}^{2}}}$|y2-y1|=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{1+{m}^{2}}$•$\sqrt{(\frac{-6m}{3{m}^{2}+4})^{2}-4•\frac{-9}{3{m}^{2}+4}}$=12•$\frac{{m}^{2}+1}{3{m}^{2}+4}$,
则$\frac{|PQ|}{|FN|}$=$\frac{4\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=$\frac{4}{\sqrt{\frac{9{m}^{4}+16+24{m}^{2}}{{m}^{2}+1}}}$,
令t=m2+1,即m2=t-1(t>1),
即有y=$\frac{9{m}^{4}+16+24{m}^{2}}{{m}^{2}+1}$=$\frac{9(t-1)^{2}+16+24(t-1)}{t}$=9t+$\frac{1}{t}$+6,
y′=9-$\frac{1}{{t}^{2}}$>0,可得函数y在(1,+∞)为增函数,
则y>9+1+6=16,
则0<$\frac{|PQ|}{|FN|}$<$\frac{4}{4}$=1;
综上可得$\frac{|PQ|}{|FN|}$的取值范围是(0,1].
点评 本题主要考查椭圆方程的求解以及直线和椭圆的位置关系是应用,利用直线和椭圆方程联立转化为一元二次方程问题是解决本题的关键.考查学生的计算能力,运算量较大,综合性较强.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
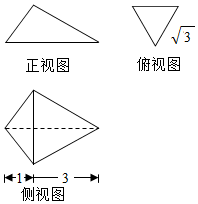
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com