
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 4$\sqrt{3}$ | D. | 16π |
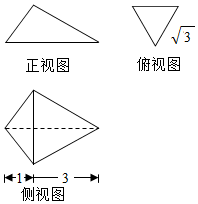
分析 由已知中的三视图,可得正视图底边对应棱的中点,到三棱锥各个顶点的距离相等,进而求出球半径,可得表面积.
解答 解:由已知中的三视图,可得该几何体的直观图如下图所示: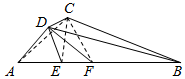
取AB的中点F,AF的中点E,
由三视图可得:AB垂直平面CDE,且平面CDE为$\sqrt{3}$的正三角形,AB=1+3=4,
∴AF=BF=2,EF=1,
∴CF=DF=$\sqrt{{1}^{2}+{\sqrt{3}}^{2}}$=2,
故F即为棱锥外接球的球心,半径R=2,
故外接球的体积S=$\frac{4}{3}$πR3=$\frac{22}{3}$π,
故选:B
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 8.5 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
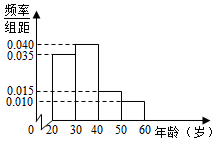 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
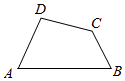 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°,则四边形ABCD的面积的最大值是3$\sqrt{3}$.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°,则四边形ABCD的面积的最大值是3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com